Adapted from P. Coles, 1999, The Routledge Critical Dictionary of the New Cosmology, Routledge Inc., New York. Reprinted with the author's permission. To order this book click here: http://www.routledge-ny.com/books.cfm?isbn=0415923549
The testing of theories of structure formation using observations of the large-scale structure of the distribution of galaxies requires a statistical approach. Theoretical studies of the problem of structure formation generally consist of performing numerical N-body simulations on powerful computers. Such simulations show how galaxies would form and cluster according to some well-defined assumptions about the form of primordial density fluctuations, the nature of any dark matter and the parameters of an underlying cosmological model, such as the density parameter and Hubble constant. The simulated Universe is then compared with observations, and this requires a statistical approach: the idea is to derive a number (a `statistic') which encapsulates the nature of the spatial distribution in some objective way. If the model matches the observations, the statistic should have the same numerical value for both model and reality. It should always be borne in mind, however, that no single statistic can measure every possible aspect of a complicated thing like the distribution of galaxies in space. So a model may well pass some statistical tests, but fail on others which might be more sensitive to particular aspects of the spatial pattern. Statistics therefore can be used to reject models, but not to prove that a particular model is correct.
One of the simplest (and most commonly used) statistical methods
appropriate for the analysis of galaxy clustering observations is the
correlation function or, more accurately, the two-point correlation
function. This measures the statistical tendency for galaxies to occur
in pairs rather than individually. The correlation function, usually
denoted by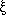 
(r),
measures the number of pairs of galaxies found at a
separation r compared with how many such pairs would be found if
galaxies were distributed at random throughout space. More formally,
the probability of finding two galaxies in small volumes
dV1 and dV2
separated by a distance r is defined to be be
dP = n2 (1 + 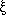(r)) dV1 dV2
where n is the average density of galaxies per unit volume. A positive
value of 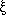(r)
thus indicates that there are more pairs of galaxies
with a separation r than would occur at random; galaxies are then said
to be clustered on the scale r. A negative value indicates that
galaxies tend to avoid each other; they are then said to be
anticlustered. A completely random distribution, usually called a
Poisson distribution, has 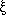(r) = 0 for all values of r.
Estimates of the correlation function of galaxies indicate that
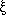(r)
is a power-law function of 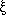r:
(r)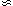 
(r/r0)-1.8
where the constant r0 is usually called the
correlation length. The
value of r0 depends slightly on the type of galaxy
chosen, but is
around 5 Mpc for bright galaxies. This behaviour indicates that these
galaxies are highly clustered on scales of up to several tens of
millions of light years in a roughly fractal pattern. On larger
scales, however,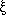
(r) becomes negative, indicating the presence of
large voids (see large-scale structure). The correlation function
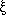(r)
is mathematically related to the power spectrum P(k) by a Fourier
transformation; the function P(k) is also used as a descriptor of
clustering on large scales.
FURTHER READING: Peebles, P.J.E., The Large-Scale Structure of the Universe (Princeton University Press, Princeton, 1980).