3.2. Searches for Massive Halos

Optical searches for massive halos are reviewed in Kormendy (1980). The current result is still that we see some changes in population and structure at large radii, but have no clear evidence that we have optically detected the massive halo component in any galaxy.

This situation is illustrated in Figure 5 by measurements of the most thoroughly studied galaxy, NGC 4565. This is an edge-on Sb with an important but not dominant bulge. We can therefore study the minor-axis bulge profile at large radii without contamination by disk light. In interpreting the profile, we would like to identify departures at large radii from an "expected" bulge profile as a new component such as the halo. Certainly the observed profile is complicated; it is nowhere described by standard fitting functions. It is tempting to interpret the outer power law beginning at 24-25 B mag arcsec^-2 as a separate component (e.g., Jensen and Thuan 1982). However, several effects make the interpretation difficult. First, the light we are measuring does not come primarily from the stars that dominate the mass density. Instead, we are measuring luminous tracers (mostly K giant stars) whose density may not be proportional to the mass density in any component if star formation properties vary with radius. The halo may or may not have such tracers. Also, it is very difficult to interpret the profile when different components overlap. Other effects, such as galaxy encounters, can also modify bulge profiles. Most important, we do not know what the profile of a bulge should be at large radii, and therefore cannot claim that a deviation from our expectation represents a new component. For example, the effect of the disk potential on bulge structure is likely to be large in a galaxy such as NGC 4565 in which the disk contributes most of the light. Furthermore bulges rotate much more rapidly than elliptical galaxies with known brightness profiles (Kormendy and Illingworth 1982a; KI). The minor axis is then a special direction, along which the structure may differ from the r^1/4 law which otherwise characterizes ellipsoidal components. The bulge of NGC 4565 rotates the flat rotation curve. Clearly minor-axis profiles alone provide only weak constraints on halo detection, except perhaps in bulgeless edge-on systems.

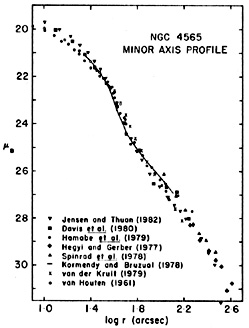Figure 5. Composite brightness profile along the minor axis of the edge-on Sb galaxy NGC 4565. Surface brightness is in B mag arcsec-2, with the zero point of Jensen and Thuan (1982). This figure does not supersede Figure 7 of Kormendy (1980), but rather complements it in that an alternative (and equally justified) averaging scheme is used. Both composite profiles are constructed by shifting the individual measurements together in µ to minimize the scatter. The results may be sensitive to the detailed behavior of that profile which is assumed to be most accurate, i.e., the one to which the others are added. In Kormendy (1980) this basic profile was the one of Davis et al. (1980); here the profiles have been combined in the order given in the key. The two composite profiles are essentially identical. This shows that small deviations from the Kormendy (1980) average of the profiles in Jensen and Thuan (1982) and in van der Kruit (1979) do not affect the conclusion that the minor-axis profile of NGC 4565 is more complicated than the usual fitting functions used to describe bulges. In particular, there is a change in shape at r ~ 50" to a power law I(r) r-2.55 at large radii.

A better way to search for halos is to measure color gradients. These provide useful constraints on the contribution of high mass-to-light ratio stars at large radii. The strongest constraints to date come from 1.25 µm R photometry by Hohlfeld and Krumm (1981). They find significant reddening outward in four nearly edge-on galaxies, but not enough reddening so that M5 and later stars can contribute most of the mass. Nevertheless, the situation is still inconclusive.

This is an observational problem which is ripe for a new and decisive attack. There appears to be a clearly best available way to measure color gradients at low light levels. To understand the special needs of this type of measurement, note first that photographic calibration errors are negligible. Wherever the galaxy image is much fainter than the sky, photography is a linear process. 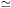It is easy to show that the relative brightness profile in mag arcsec^-2 (without zero point) is independent even of the slope of the photographic characteristic curve near sky, D log I, D the density and I the intensity. (I am indebted to Dr. I.R. King for pointing this out.) Since calibration is not a problem, errors in the derived profile come almost completely from errors in the assumed sky brightness, and especially from fluctuations in it. Photographic data, which measure all galaxy and sky pixels simultaneously, suffer from spatial fluctuations in emulsion sensitivity. Photoelectric observations, which usually measure only one pixel at a time, are acutely sensitive to temporal fluctuations in sky brightness on time scales as short as one second. Clever measuring techniques partly circumvent this problem. For example, Melnick, White and Hoessel (1977) used an auxiliary photometer to monitor sky fluctuations during the observations, and Hegyi and Gerber (1977, 1979) designed a photometer which repeatedly scans around an annulus that includes both galaxy and sky. Despite the success of these techniques, photoelectric photometry is still inefficient, because only one pixel is measured at a time. Its most valuable service is probably to provide accurate measurements at a few points in the image, to calibrate and check photographic data. At present the best way to measure color gradients in galaxy halos appears to be a variation of the "grid photometry" technique developed by Davis, Feigelson and Latham (1980). This uses a mask in contact with the plate to cover alternate narrow strips across the image. After the object exposure the mask is shifted to uncover these strips and cover the exposed ones. An exposure on blank sky then allows calibration of the sensitivity variations throughout the image. Accurate color maps could now be derived using emulsions such as Kodak 098-04, which are sensitive in both the blue and the red. Three alternating strips could be used, exposed to (say) the U image, the R image and a uniform background. Tests would be necessary to see whether sensitivity variations need to be mapped separately in U and R. It would also be necessary to optimize the measurements in the usual way, e.g. by taking many plates and keeping only the best, and by using a telescope which provides uniform illumination. At surface brightnesses below ~ 29 - 30 mag arcsec^-2, light scattered by the emulsion and telescope optics might also require a correction (see King 1971; Kormendy 1973). Given sufficient care it should be possible to measure accurate colors to ~ 28 B mag arcsec^-2, and thereby put much stronger constraints on the contribution of lowmass stars to galaxy halos.