


Detailed reviews of gas velocity fields have been published by van der Kruit and Allen (1978), Faber and Gallagher (1979), Rubin (1979a, b, 1982), Bosma (1981b, 1982), and others. To save space, I will confine my discussion to the kinematic evidence for large amounts of dark matter in galaxies.
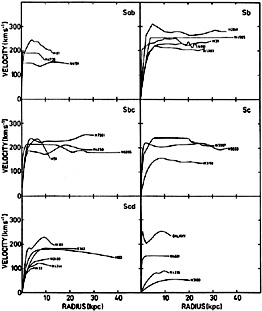 |
Figure 30. Combined optical and H I rotation curves for galaxies of various Hubble types, from Bosma (1978, 1981b). The measurements reach an average radius of 2.1 (dispersion = 1.2) times the radius of the 25 B mag arcsec-2 contour. Near the center, the resolution of many observations is inadequate, and the curves are schematic. At large radii, many curves are affected by oval distortions, warps, asymmetries and interactions with other galaxies (see the above references). Distances are calculated using H0 = 75 km s-1 Mpc-1. A similar figure showing flat rotation curves from optical measurements is given in Rubin, Ford and Thonnard (1980). |
It is now well known that galaxy rotation curves are flat out to
remarkably large radii (e.g., Fig. 30). I am
not aware of any
unambiguous measurements of falling rotation curves, i.e., ones which
clearly indicate that most of the mass is interior to the outermost
point measured (see
Rubin 1979a,
b).
If V(r) 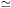 constant, very simple
and general arguments indicate that there are large amounts of unseen
mass in galaxies, especially at large radii. The following discussion
assumes a spherical galaxy; if the mass distribution is flattened, the
amount of material required is changed by less than a factor of two
(Krumm and Salpeter
1977,
see also
Bahcall, Schmidt and
Soneira 1982).
For test particles in circular orbits in a spherical potential,
V2 / r = GM(r) /
r2, where M(r) is the mass contained
within radius r, and G is
the gravitational constant. The consequences of a V = constant
rotation curve are,
constant, very simple
and general arguments indicate that there are large amounts of unseen
mass in galaxies, especially at large radii. The following discussion
assumes a spherical galaxy; if the mass distribution is flattened, the
amount of material required is changed by less than a factor of two
(Krumm and Salpeter
1977,
see also
Bahcall, Schmidt and
Soneira 1982).
For test particles in circular orbits in a spherical potential,
V2 / r = GM(r) /
r2, where M(r) is the mass contained
within radius r, and G is
the gravitational constant. The consequences of a V = constant
rotation curve are,
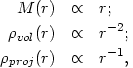 |
(15) |
where
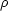 vol
and
vol
and
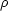 proj
are the unprojected and projected mass densities.
The linear rise of M(r) with r is illustrated in Figure 6 of
Rubin, Ford and
Thonnard (1978b),
in Figure 5 of
Bosma (1981b),
and in Figure 3 of
Burstein et al. (1982).
There is no sign that M(r) is
beginning to converge on a total mass. While
proj
are the unprojected and projected mass densities.
The linear rise of M(r) with r is illustrated in Figure 6 of
Rubin, Ford and
Thonnard (1978b),
in Figure 5 of
Bosma (1981b),
and in Figure 3 of
Burstein et al. (1982).
There is no sign that M(r) is
beginning to converge on a total mass. While
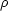 proj
proj
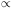 r-1, the
projected surface brightness is decreasing much more rapidly, like
1.7
r-1, the
projected surface brightness is decreasing much more rapidly, like
1.7 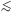 n
n
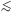 2 in ellipticals
and like e-r/r0 (or even faster) in
spirals. Necessarily, then, the local mass-to-light ratio M/L
increases with increasing radius. This important result is illustrated
in Figure 31
(Bosma 1978,
1981b).
Similar results are derived by
Krumm and Salpeter
(1977),
Schweizer (1978a),
Rubin et al. (1978a),
Peterson et
al. (1978b),
Bosma and van der Kruit
(1979),
Petrou (1981) and
Burstein et al. (1982).
Flat rotation curves and hence M/L ratios
which increase outward are also seen in absorption-line measurements of
S0 galaxies (e.g., NGC 4762,
Illingworth 1981;
NGC 3115,
Illingworth and
Schechter 1982,
and references therein; NGC 1553,
Figure 47). The
same is true for barred galaxies
(section 5.1.3), an interesting result in
view of the fact that massive envelopes were proposed on theoretical
grounds in order to get rid of bars
(Ostriker and Peebles
1973).
Kinematic data on ellipticals are consistent with the presence of
massive envelopes (see
Gunn 1980
for a review, also section 4.2.5), but
do not make a strong statement, because there is little gas to give a direct
measure of the mass distribution (e.g.,
Raimond et al. 1981).
However, other techniques, especially X-ray observations, indicate that
there are massive halos in at least some (possibly special?) galaxies
(e.g., M87:
Bahcall and Sarazin
1977;
Mathews 1978;
Fabricant, Lecar and
Gorenstein 1980,
but contrast
Binney and Cowie 1981).
Further discussion of the importance of halos as a function of Hubble
type is given in section 2.3.
2 in ellipticals
and like e-r/r0 (or even faster) in
spirals. Necessarily, then, the local mass-to-light ratio M/L
increases with increasing radius. This important result is illustrated
in Figure 31
(Bosma 1978,
1981b).
Similar results are derived by
Krumm and Salpeter
(1977),
Schweizer (1978a),
Rubin et al. (1978a),
Peterson et
al. (1978b),
Bosma and van der Kruit
(1979),
Petrou (1981) and
Burstein et al. (1982).
Flat rotation curves and hence M/L ratios
which increase outward are also seen in absorption-line measurements of
S0 galaxies (e.g., NGC 4762,
Illingworth 1981;
NGC 3115,
Illingworth and
Schechter 1982,
and references therein; NGC 1553,
Figure 47). The
same is true for barred galaxies
(section 5.1.3), an interesting result in
view of the fact that massive envelopes were proposed on theoretical
grounds in order to get rid of bars
(Ostriker and Peebles
1973).
Kinematic data on ellipticals are consistent with the presence of
massive envelopes (see
Gunn 1980
for a review, also section 4.2.5), but
do not make a strong statement, because there is little gas to give a direct
measure of the mass distribution (e.g.,
Raimond et al. 1981).
However, other techniques, especially X-ray observations, indicate that
there are massive halos in at least some (possibly special?) galaxies
(e.g., M87:
Bahcall and Sarazin
1977;
Mathews 1978;
Fabricant, Lecar and
Gorenstein 1980,
but contrast
Binney and Cowie 1981).
Further discussion of the importance of halos as a function of Hubble
type is given in section 2.3.
 |
Figure 31. Radial variations of the local mass-to-light ratio, from Bosma (1978, 1981b) and Bosma and van der Kruit (1979). The luminosity data have not been corrected for internal or Galactic absorption except in IC 342 (AB = 2.2 mag). Distances are based on H0 = 75 km s-1 Mpc-1. |
Thus there is a great deal of direct evidence for unseen, massive envelopes in galaxies. Further indirect evidence is discussed in Faber and Gallagher (1979). The need now is for data and models which are accurate enough so that we can determine the properties of these halos. It is clear that they are larger than visible galaxies, but what are their core radii? How does the halo mass depend on galaxy mass and type? Are halos triaxial, and if so, what effect does this have? Can the answers to these questions put useful constraints on the composition of halos?