

Massive stars contain many of the extremes of astrophysics. Their high
masses result in high luminosities, with energy outputs on the order of
a million times that of the sun. While on the main-sequence as O-type
stars, they have nearly the highest effective temperatures of any stars,
with only white dwarfs being hotter. As Luminous Blue Variables (LBVs),
they show spectacular outbursts, throwing off large amount of material
and brightening by several magnitudes visually. As yellow supergiants
(YSGs), they are among the visually brightest in any galaxy, although,
ironically, their identification is often complicated by the plethora of
foreground Galactic yellow dwarfs. As cool red supergiants (RSGs), they
flirt with the limits of hydrostatic equilibrium, and are physically the
largest stars: if you place one of the biggest at the center of the
solar system, its photosphere would end somewhere between the orbits of
Jupiter and Saturn. As Wolf-Rayets (WRs) they are little more than
stripped stellar cores with such strong stellar winds that they would
lose ten times the mass of the sun in a mere million years, were they to
live that long. Finally, massive stars end their lives as spectacular
supernova, briefly outshining the whole of their host galaxies.
There are two fundamental reasons for studying massive stars amongst the
star-forming galaxies of the Local Group. First, these galaxies allow us
to perform tests of stellar evolutionary theory in a laboratory where
primarily a single variable can be changed, namely the chemical
composition of the stars. The physical properties of a massive star
will be essentially identical at birth regardless of small changes in
the composition. (Recall that the heavier elements represent only a few
percent of the overall composition of stars.) But, these trace elements
have a large impact on the subsequent evolution of massive stars. On the
main-sequence, a massive star's high effective temperature and
luminosity result in strong stellar winds, which are driven by radiation
pressure on these highly ionized metal atoms, resulting in significant
mass loss. A 100
M star
could lose half of its
mass during its short lifetime! The importance of this mass-loss on mass
star evolution was first demonstrated by the early models that attempted
to include the effects of mass loss (e.g.,
de Loore et al. 1977,
1978;
Chiosi et al. 1978,
1979;
Brunish & Truran
1982).
Modern models continue to demonstrate the importance of mass loss to
massive star evolution
(Meynet & Maeder
2005).
Because these winds are driven by
radiation pressure acting on highly ionized metal atoms, the mass-loss
rates
star
could lose half of its
mass during its short lifetime! The importance of this mass-loss on mass
star evolution was first demonstrated by the early models that attempted
to include the effects of mass loss (e.g.,
de Loore et al. 1977,
1978;
Chiosi et al. 1978,
1979;
Brunish & Truran
1982).
Modern models continue to demonstrate the importance of mass loss to
massive star evolution
(Meynet & Maeder
2005).
Because these winds are driven by
radiation pressure acting on highly ionized metal atoms, the mass-loss
rates  depend upon a star's initial metallicity z, as
something like
depend upon a star's initial metallicity z, as
something like  ~ z0.7
(Vink et al. 2001).
Thus, over the ~ 20× metallicity difference between WLM (z /
z
~ z0.7
(Vink et al. 2001).
Thus, over the ~ 20× metallicity difference between WLM (z /
z ~ 0.1)
to M31
(z /
z
~ 0.1)
to M31
(z /
z ~ 2),
we expect the main-sequence mass-loss rates to vary by nearly an order of
magnitude. Such differences should be (and are) reflected in the
relative number of evolved massive stars of various kinds, such as the
relative number of Wolf-Rayet stars to red supergiants, or the relative
number of WC- and WN-type WRs.
~ 2),
we expect the main-sequence mass-loss rates to vary by nearly an order of
magnitude. Such differences should be (and are) reflected in the
relative number of evolved massive stars of various kinds, such as the
relative number of Wolf-Rayet stars to red supergiants, or the relative
number of WC- and WN-type WRs.
Secondly, these massive stars affect the overall evolution and properties of the galaxies themselves, through three "feedback" mechanisms (see, e.g., Oey & Clarke 2009). First, their ultraviolet radiation heats dust, powering the far-IR luminosities of galaxies, while at the same time providing the ionizing radiation that causes the HII regions (see, e.g., Maeder & Conti 1994). Of course, it is these HII regions which delineate the arms in spiral galaxies, and otherwise reveal where most of the star formation action is occurring in irregular galaxies. Secondly, their strong stellar winds provide significant mechanical energy input into the interstellar medium, as does their eventual disruption as supernovae (Abbott 1982), shock-heating the gas to > 106 K (Oey & Clarke 2009). This mechanical energy feedback is responsible for the creation of superbubbles (Pikel'ner 1968; Weaver et al. 1977; see discussion in Oey et al. 2001). And thirdly, they are responsible for much of the chemical enrichment of galaxies, particularly of the "lighter" elements (atomic weight less than 30), such as carbon, nitrogen, and oxygen (Maeder 1981, Sparke & Gallagher 2000). During their red supergiant phase, massive stars also make a significant contribution to the dust content, particularly for star-burst systems and galaxies at large look-back times where AGBs have not yet formed (Massey et al. 2005a).
In this review, we will first provide an introduction to massive stars, and then follow this with a more detailed description of the current state of our knowledge (and lack thereof) of the content of these stars in Local Group galaxies. A much shorter review on this subject was given by Massey (2010), and an older, but more detailed look, can be found in Massey (2003).
When we talk about the "star-forming galaxies of the Local Group," we are referring to the galaxies listed in Table 1, an updated version of Table 1 from Massey (2003) and Massey et al. (2007b).
| Galaxy | Type | l | b | MV | E(B-V) b | Dist (Mpc) | log O/H+12 |
| MW | S(B)bc I-II: | — | — | -20.9? | — | — | 8.7 c |
| M31 | Sb I-II | 121.2 | -21.6 | -21.2 | 0.13 | 0.76 | 8.9-9.0 d |
| M33 | Sc II-III | 133.6 | -31.3 | -18.9 | 0.12 | 0.83 | 8.3-8.9 e |
| LMC | Ir III-IV | 280.2 | -33.3 | -18.5 | 0.13 | 0.050 | 8.4 |
| SMC | Ir IV-V | 302.8 | -44.3 | -17.1 | 0.09 | 0.059 | 8.0 |
| NGC 6822 | Ir IV-V | 25.3 | -18.4 | -16.0 | 0.25 | 0.50 | 8.1 |
| IC 10 | Ir IV: | 119.0 | -3.3 | -16.3 | 0.81 | 0.66 | 8.2 |
| IC 1613 | Ir V | 129.7 | -60.6 | -15.3 | 0.72 | 0.05 f | 7.9 |
| WLM | Ir IV-V | 75.9 | -73.6 | -14.4 | 0.07 | 0.93 | 7.7 |
| Pegasus | Ir V | 94.8 | -43.6 | -12.3 | 0.15 | 0.76 | 7.9 |
| Phoenix | dIr/dSph | 272.2 | -69.0 | -9.8 | 0.15 | 0.40 | — |
| a Data from van den Bergh (2000) and references therein, except as noted. | |||||||
| b From Massey et al. (2007b), except as noted. | |||||||
| c In the solar neighborhood. | |||||||
| d From Sanders et al. (2012) at R = 12 kpc. | |||||||
| e From Magrini et al. (2007) but see Bresolin (2011) and discussion in Neugent & Massey (2011). | |||||||
| f From Sandage (1971). | |||||||
Before delving into the primer, it is worth emphasizing that our understanding of massive star properties and evolution derives not from observations or theory alone, but from the combination of the two: even something as basic as a star's luminosity relies not only upon the visual brightness, but also a knowledge of stellar atmospheres in order to relate what is observed to the meaningful physical quantity. Within this review, a lot of the emphasis will be given to the observational side, but it would be horribly remiss not to stress the importance of theory as well. Just as large telescopes and more efficient detectors have made possible observations only dreamed of in the 1960s, so has the improvement in the physics and computational tools improved both the study of stellar atmospheres and stellar evolution. Further, just as observers often go to pains to make their data freely available, our theoretician colleagues have gone to similar efforts to share the results of their modeling and codes. The first non-LTE atmosphere modeling that included only H and He done by Auer & Mihalas (1972) have now evolved to very complex non-LTE codes that include the effects of line-blanketing and stellar winds, such as CMFGEN (Hillier & Miller 1998), a code which is made publicly available by the kindness of D. John Hillier. Similarly, the early evolutionary models that included the effects of mass loss have now evolved to very sophisticated models that include the effects of rotation and mass loss throughout the H-R diagram (e.g., Maeder & Meynet 2000a, 2000b; Meyent & Maeder 2000, 2003, 2005; Ekström et al. 2012; Georgy et al. 2012). The Geneva group has, in particular, always been very generous by making their models publicly available, encouraging direct comparisons (and sometimes confrontations) between predictions and observations.
Evolution.
Massive stars (m >
8M )
begin their lives on the main-sequence as
O- and early B-type dwarfs. As these stars age,
they burn hydrogen in their cores via the CNO cycle. The main-sequence
(hydrogen-burning) phase lasts for between 3 Myr (120
M
)
begin their lives on the main-sequence as
O- and early B-type dwarfs. As these stars age,
they burn hydrogen in their cores via the CNO cycle. The main-sequence
(hydrogen-burning) phase lasts for between 3 Myr (120
M ) and
30 Myr (9
M
) and
30 Myr (9
M ),
according to the latest solar-metallicity Geneva models
(Ekström et
al. 2012).
We summarize some of their main-sequence properties in
Table 2, where we have assigned
spectral types and luminosity classes based upon their evolutionary
effective temperatures and surface gravities. There are several things
of note:
),
according to the latest solar-metallicity Geneva models
(Ekström et
al. 2012).
We summarize some of their main-sequence properties in
Table 2, where we have assigned
spectral types and luminosity classes based upon their evolutionary
effective temperatures and surface gravities. There are several things
of note:
 to ~
85 M
to ~
85 M .
.
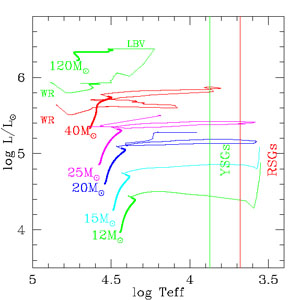 |
Figure 1. Evolution of massive stars. The
high mass Geneva evolutionary tracks
(Ekström et
al. 2012)
for solar metallicity (z = 0.014) are shown ; these models assume an
initial rotation velocity of 40% of the critical break-up speed.
The initial masses label the beginning part of each track; for
simplicity we have not included the
85 M |
| ZAMS | Turn-off | Start of He-burning | |||||||||||||
| Mass | tH | Teff | Log | Log g | Spect. | Teff | Log | Log g | Spect. | Teff | Log | Log g | Spect. | ||
M |
(Myr) | (K) | L/L |
[cgs] | Type | (K) | L/L |
[cgs] | Type | (K) | L/L |
[cgs] | Type | ||
| 120 | 3.2 | 52,000 | 6.2 | 4.1 | O2-3 V | 50,500 | 6.2 | 4.0 | O2-3 V | 29,400 | 6.0 | 2.8 | B0 I | ||
| 85 | 3.7 | 50,000 | 6.0 | 4.2 | O2-3 V | 48,000 | 6.0 | 4.0 | O2-3 V | 21,300 | 6.3 | 2.1 | B1 I | ||
| 60 | 4.4 | 47,000 | 5.7 | 4.2 | O3 V | 45,000 | 5.8 | 4.0 | O4 V | 7,100 | 6.1 | 0.2 | F5 I | ||
| 40 | 5.7 | 43,000 | 5.3 | 4.2 | O4 V | 31,500 | 5.7 | 3.2 | O9 I | 6,400 | 5.9 | 0.2 | F8 I | ||
| 25 | 7.9 | 38,000 | 4.9 | 4.2 | O6 V | 27,300 | 5.3 | 3.2 | B0.2 I | 7,900 | 5.4 | 0.9 | F0 I | ||
| 20 | 9.5 | 35,000 | 4.6 | 4.3 | O7.5 V | 25,800 | 5.0 | 3.3 | B0.5 I | 12,300 | 5.1 | 1.9 | B6 I | ||
| 15 | 13.5 | 31,000 | 4.3 | 4.3 | O9.5 V | 24,300 | 4.7 | 3.4 | B0.5 I | 9,500 | 4.8 | 1.6 | A0 I | ||
| 12 | 18.4 | 27,900 | 4.0 | 4.3 | B0.5 V | 22,300 | 4.4 | 3.5 | B0.5 I | 8,200 | 4.5 | 1.7 | A8 I | ||
| 9 | 31.2 | 24,000 | 3.6 | 4.3 | B1 V | 19,600 | 4.0 | 3.5 | B1.5 III | 3,800 | 4.1 | 0.6 | M0 I | ||
| a Based on Ekström et al. (2012), Massey et al. (2005b), and Levesque et al. (2007). | |||||||||||||||
There are a few other caveats that need to be kept in mind when talking
about the main-sequence evolution of massive stars.
First, the luminosity class ("I" vs "V", say) of O-type stars depends
primarily on lines that are not so much sensitive to
surface gravity but rather to stellar wind strengths. The higher the
bolometric luminosity at a given
metallicity, the stronger the stellar wind will be
( ~
L2.1, according to
Vink et al. 2000,
for Teff > 27,500 K),
as there is only a weak dependence upon the effective temperature
in the mass-loss rates for stars this hot
1.
So, stars in the high mass and luminosity range will have the strongest
mass-loss rates.
The luminosity class is primarily based upon the morphology of the He II
~
L2.1, according to
Vink et al. 2000,
for Teff > 27,500 K),
as there is only a weak dependence upon the effective temperature
in the mass-loss rates for stars this hot
1.
So, stars in the high mass and luminosity range will have the strongest
mass-loss rates.
The luminosity class is primarily based upon the morphology of the He II
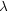 4686 line. This line
is both sensitive to mass-loss rates
and effective temperatures, and (for a given spectral subtype) a
He II
4686 line. This line
is both sensitive to mass-loss rates
and effective temperatures, and (for a given spectral subtype) a
He II 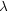 4686
line that is strongly in absorption leads
to a luminosity class "V", while one in emission leads to a luminosity
class "I". When He II
4686
line that is strongly in absorption leads
to a luminosity class "V", while one in emission leads to a luminosity
class "I". When He II
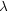 4686 is in emission,
along with the neighboring N III
4686 is in emission,
along with the neighboring N III
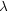 4634, 42 line, we
call the O star an "Of-type", with the implication that the star is of
luminosity class "I". (The actual system is a bit more complicated than
this; see, e.g.,
Sota et al. 2011.)
The NIII emission behavior has finally been demonstrated to be dependent
on stellar wind strengths, although nitrogen abundance also plays an
important role
(Rivero Gonzáez et
al. 2011).
Of course, a significant problem occurs when one looks at O stars in
other galaxies that are more metal-poor than the Milky Way where the
various spectral standards have been defined. Even a high-luminosity O
star in the SMC may fail to show He II
4634, 42 line, we
call the O star an "Of-type", with the implication that the star is of
luminosity class "I". (The actual system is a bit more complicated than
this; see, e.g.,
Sota et al. 2011.)
The NIII emission behavior has finally been demonstrated to be dependent
on stellar wind strengths, although nitrogen abundance also plays an
important role
(Rivero Gonzáez et
al. 2011).
Of course, a significant problem occurs when one looks at O stars in
other galaxies that are more metal-poor than the Milky Way where the
various spectral standards have been defined. Even a high-luminosity O
star in the SMC may fail to show He II
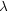 4686 and be labeled a
"giant" or even a "dwarf", when its absolute visual magnitude
demonstrates it's a supergiant; see discussion in
Massey et al. (2005b).
4686 and be labeled a
"giant" or even a "dwarf", when its absolute visual magnitude
demonstrates it's a supergiant; see discussion in
Massey et al. (2005b).
The other thing to keep in mind about the evolutionary models is that
they are static, not hydrodynamic. Note that in
Table 2
I assigned a spectral type of B0 I to the
120 M star at the start of He-burning, but
the situation may be a little more complicated than that. These stars
will have such high mass-loss rates that it is possible, even likely,
that the 120
M
star at the start of He-burning, but
the situation may be a little more complicated than that. These stars
will have such high mass-loss rates that it is possible, even likely,
that the 120
M star
will not be identified as an
O3-4 V or B0 I, but rather as a hydrogen-rich, WN Wolf-Rayet star,
similar to the highest mass (but unevolved) stars seen in the R136
cluster in the LMC and NGC 3603 in
the Milky Way: "Of-type stars on steroids"
(Crowther et al. 1995,
Massey & Hunter
1998).
star
will not be identified as an
O3-4 V or B0 I, but rather as a hydrogen-rich, WN Wolf-Rayet star,
similar to the highest mass (but unevolved) stars seen in the R136
cluster in the LMC and NGC 3603 in
the Milky Way: "Of-type stars on steroids"
(Crowther et al. 1995,
Massey & Hunter
1998).
Stellar Winds One of the areas of active research is the issue of what the mass-loss rates are during the hot main-sequence stage. Historically, there have been three methods for measuring the mass-loss rates in O-type stars:
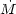 × q, where
q is the ion fraction of the species. But even if one knows
q to high accuracy, mostly these lines are saturated, leading
to only lower limits on
× q, where
q is the ion fraction of the species. But even if one knows
q to high accuracy, mostly these lines are saturated, leading
to only lower limits on
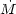 .
.
 emission profile, superposed upon photospheric absorption
(Klein & Castor 1978,
Leitherer 1988,
Lamers & Leitherer
1993).
This method has often been considered to be more accurate than (1),
leading to values that are 10% or better. But, one still needs to get
everything else right including the velocity law, especially if the
winds are weak and hidden in photospheric
H
emission profile, superposed upon photospheric absorption
(Klein & Castor 1978,
Leitherer 1988,
Lamers & Leitherer
1993).
This method has often been considered to be more accurate than (1),
leading to values that are 10% or better. But, one still needs to get
everything else right including the velocity law, especially if the
winds are weak and hidden in photospheric
H . In those cases the method is probably a factor of 2
uncertain.
. In those cases the method is probably a factor of 2
uncertain.
Both the H and IR/radio
continua methods rely upon the interaction
of two particles, and they are therefore referred to as "density-squared"
(
and IR/radio
continua methods rely upon the interaction
of two particles, and they are therefore referred to as "density-squared"
(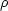 2)
processes. In contrast, P Cygni lines are due to scattering; i.e., a
photon is absorbed and immediately re-emitted. In general, the results
from the two
2)
processes. In contrast, P Cygni lines are due to scattering; i.e., a
photon is absorbed and immediately re-emitted. In general, the results
from the two
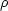 2
processes agreed, but with the occasional pathological cases
(Lamers & Leitherer
1993,
Puls et al. 1996).
This happy state of affairs was changed when
Fullerton et al. (2006)
used the FUSE satellite to measure the mass-loss rates from the
P V
2
processes agreed, but with the occasional pathological cases
(Lamers & Leitherer
1993,
Puls et al. 1996).
This happy state of affairs was changed when
Fullerton et al. (2006)
used the FUSE satellite to measure the mass-loss rates from the
P V 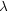
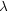 118, 28
resonance doublet. This side stepped the saturation problem with the P
Cygni profiles: since phosphorus is rare, the line isn't saturated. They
found mass-loss rates which were, at first blush,
a factor of 10 lower than what had been assumed previously with the
assumption of homogeneous, spherically symmetric winds. Instead, it now
accepted that stellar winds are "clumped", and not as homogeneous as had
been assumed for convenience. As
Fullerton et al. (2008)
wrote, "Thus, a fundamental consequence of clumping in hot-star winds is
that the values of
118, 28
resonance doublet. This side stepped the saturation problem with the P
Cygni profiles: since phosphorus is rare, the line isn't saturated. They
found mass-loss rates which were, at first blush,
a factor of 10 lower than what had been assumed previously with the
assumption of homogeneous, spherically symmetric winds. Instead, it now
accepted that stellar winds are "clumped", and not as homogeneous as had
been assumed for convenience. As
Fullerton et al. (2008)
wrote, "Thus, a fundamental consequence of clumping in hot-star winds is
that the values of
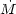 (
( 2)
must be reduced. The only question is: by how much?" Naively, all
other things being equal, the answer would be a factor of ten
but current thinking now is that generally the value is more likely a
factor of 2 or 3
(Hirschi 2008,
Puls et al. 2008).
But this remains one of the great uncertainties that motivates
observational comparisons of the relative number of massive stars in
various stages versus what is predicted by the evolutionary models with
some assumed mass-loss rate.
2)
must be reduced. The only question is: by how much?" Naively, all
other things being equal, the answer would be a factor of ten
but current thinking now is that generally the value is more likely a
factor of 2 or 3
(Hirschi 2008,
Puls et al. 2008).
But this remains one of the great uncertainties that motivates
observational comparisons of the relative number of massive stars in
various stages versus what is predicted by the evolutionary models with
some assumed mass-loss rate.
Knowing the number of progenitor, main-sequence stars relative to the number of their evolved descendants provides a key observational test of stellar evolutionary models, but as we will see in Section 2.1, quantifying this is among the most difficult observational challenges, as the main-sequence phase is when massive stars are the visually faintest.
What happens after the main-sequence, depends upon the mass of the star. For the highest mass stars, they encounter a little difficulty as they edge to cooler temperatures: the opacities of the lines increase as the temperatures decrease, and soon radiation pressure equals or exceeds the force of gravity (Lamers 1997). This point is probably associated with the phase known as the classic "Luminous Blue Variables," previously known as Hubble-Sandage variables (Hubble & Sandage 1953) or "S Doradus" variables. Of all the various phases through which a massive star passes, the details and implications of the LBV phase are probably the most poorly understood. What is generally agreed upon is that the "classic" LBVs, such as S Doradus and P Cygni, undergo giant "eruptions" every few hundred years, in which there are large photometric changes (several magnitudes) accompanied by large amounts of material coming off of the star (see, e.g., Bohannan 1997 and Conti 1997).
The star  Car is often cited as the prototypical LBV. It certainly
has been the most heavily studied both ground-based and space-based
(e.g., HST): the SAO/NASA Astrophysics Data System reports nearly
500 refereed papers containing
Car is often cited as the prototypical LBV. It certainly
has been the most heavily studied both ground-based and space-based
(e.g., HST): the SAO/NASA Astrophysics Data System reports nearly
500 refereed papers containing
 Car in its
title, and over 1200 if conference proceedings are counted as well. Beyond
question it is an interesting object in its own right, but
Car in its
title, and over 1200 if conference proceedings are counted as well. Beyond
question it is an interesting object in its own right, but
 Car is
probably not much of a rosetta stone for LBVs in general, as it consists
of a 5.5 year binary. The stars are in an eccentric orbit,
and some have argued that the major eruptions have been triggered by
mass transfer at periastron passage (see, e.g.,
Kashi & Soker 2010).
The discovery of the binary nature of the system has been relatively
recent
(van Genderen et
al. 1994,
Damineli et al. 1997,
Sonneborn et al. 2005),
and has led to a series of observing campaigns at each new close passage.
Car is
probably not much of a rosetta stone for LBVs in general, as it consists
of a 5.5 year binary. The stars are in an eccentric orbit,
and some have argued that the major eruptions have been triggered by
mass transfer at periastron passage (see, e.g.,
Kashi & Soker 2010).
The discovery of the binary nature of the system has been relatively
recent
(van Genderen et
al. 1994,
Damineli et al. 1997,
Sonneborn et al. 2005),
and has led to a series of observing campaigns at each new close passage.
Smith & Owocki (2006)
suggest that, if the main-sequence mass-loss rates are actually ~
10× lower than they the unclumped models indicate (rather than the
2-3×
Puls et al. 2008
and others have argued must be the case), the mass loss during the LBV
phase may be critically important to the further evolution of massive
stars.
Smith et al. (2004)
argue for the existence of "lower mass" LBVs, as low as 10-15
M , whose
winds become sufficiently strong at an
effective temperature of 21,000 K to cause "pseudo-photospheres" to
form, mimicking (at least) the behavior of many high luminosity
LBVs. (The 21,000 K effective temperature corresponds to the
"bistability jump", where a small drop in effective temperature results
in a decrease in the ionization of the wind, leading to a smaller, but
much denser, stellar wind. See
Pauldrach & Puls 1990
and
Lamers et al. 1995.)
But, much of this is conjecture.
, whose
winds become sufficiently strong at an
effective temperature of 21,000 K to cause "pseudo-photospheres" to
form, mimicking (at least) the behavior of many high luminosity
LBVs. (The 21,000 K effective temperature corresponds to the
"bistability jump", where a small drop in effective temperature results
in a decrease in the ionization of the wind, leading to a smaller, but
much denser, stellar wind. See
Pauldrach & Puls 1990
and
Lamers et al. 1995.)
But, much of this is conjecture.
What is clear is that due to the length of time between major outbursts, it is very tough to get a good handle on the number of LBVs. The spectra of "hot" LBVs show emission of [FeII], He I, and the Balmer lines, while the latter two series usually display P Cygni profiles (see, for example, Figure 10 in Massey et al. 2007a). Their spectra can instead resemble those of P Cygni itself, with strong Balmer and He I P Cygni emission but no forbidden Fe. During their cool phase they can develop a "pseudo-photosphere", and their spectra resemble that of a late G- or F-type supergiant with strong Balmer emission. The "hot" phase is often described as their "quiescence" stage, and their "cool" phase as an "outburst" stage, but an accidental spectrum of S Dor itself in 1999 revealed the coolest spectrum in 50 years of spectroscopic monitoring; the F-type "pseudo-photosphere" was not accompanied by any major change in its photometry (Massey 2000). Of course, that may require several hundred years (see discussion in Massey 2006). We will discuss this further in Section 2.2.
1.3.1. Red and Yellow Supergiants
Stars of somewhat lower mass (< 30
M ?) will
evolve quickly to the red, passing
first through a yellow supergiant phase. It is in this stage that a
massive star will be at its visually brightest, with the peak of the
flux distribution being at visible wavelengths. (Recall that stellar
evolution of massive stars takes place at nearly constant bolometric
luminosity, so as the star cools to temperatures
similar to those of the Sun, their visual brightness will peak.) The YSG
phase is so short (a few thousand to a few tens of thousands
of years), that the phase has little evolutionary implications (i.e., in
terms of mass loss), but as we shall see in
Section 2.3 this phase acts as a very
sensitive probe of the accuracy of earlier evolutionary calculations.
?) will
evolve quickly to the red, passing
first through a yellow supergiant phase. It is in this stage that a
massive star will be at its visually brightest, with the peak of the
flux distribution being at visible wavelengths. (Recall that stellar
evolution of massive stars takes place at nearly constant bolometric
luminosity, so as the star cools to temperatures
similar to those of the Sun, their visual brightness will peak.) The YSG
phase is so short (a few thousand to a few tens of thousands
of years), that the phase has little evolutionary implications (i.e., in
terms of mass loss), but as we shall see in
Section 2.3 this phase acts as a very
sensitive probe of the accuracy of earlier evolutionary calculations.
At the coolest temperatures, these < 30
M stars are red supergiants, the physically largest stars.
Levesque (2010,
2012)
has recently reviewed their physical properties. For many years, their
"observed" locations in the H-R diagram (HRD) were much cooler and more
luminous than stellar evolutionary theory allowed, although few
researchers seemed to realize this. The basic problem was that the
effective temperatures were derived primarily from lunar occultations of
red giants (see discussion in
Massey & Olsen 2003).
The use of the new MARCS models
(Gustafsson et al. 1975,
Plez et al. 1992),
which included sphericity and improved molecular opacities for TiO and
other oxygen-rich molecules
(Plez 2003,
Gustafsson et al. 2003,
Gustafsson et al. 2008),
led to effective temperatures and luminosities that agreed well with the
Geneva models over a wide range of metallicities
(Levesque et al. 2005,
2006;
Massey et al. 2009).
stars are red supergiants, the physically largest stars.
Levesque (2010,
2012)
has recently reviewed their physical properties. For many years, their
"observed" locations in the H-R diagram (HRD) were much cooler and more
luminous than stellar evolutionary theory allowed, although few
researchers seemed to realize this. The basic problem was that the
effective temperatures were derived primarily from lunar occultations of
red giants (see discussion in
Massey & Olsen 2003).
The use of the new MARCS models
(Gustafsson et al. 1975,
Plez et al. 1992),
which included sphericity and improved molecular opacities for TiO and
other oxygen-rich molecules
(Plez 2003,
Gustafsson et al. 2003,
Gustafsson et al. 2008),
led to effective temperatures and luminosities that agreed well with the
Geneva models over a wide range of metallicities
(Levesque et al. 2005,
2006;
Massey et al. 2009).
The amount of mass lost during the RSG phase is a key factor in determining what happens next to the star; it is also one of factors most poorly constrained by observation and theory (Georgy et al. 2013). High mass loss during this stage will shorten the RSG phase, and cause the star to evolve bluewards again in the HRD, going through a second YSG phase possibly becoming a Wolf-Rayet star or even an LBV (Groh et al. 2013). Otherwise, RSGs are expected to end their lives as Type II supernovae.
RSGs are "smokey": dust condenses as the star loses mass. Recently this led to the realization that RSGs suffer significant circumstellar reddening (see, e.g., Massey et al. 2005a). Little is understood about what drives this mass loss. Massey et al. (2008) quotes Stan Owocki (2007, private communication) as arguing that it doesn't take much to "drive" a RSG wind. The escape velocity from a star is just 620 km s-1 × (M / R)1/2. Although O stars have a M/R ratio that is of order unity, RSGs do not: the ratio is much smaller, more like 0.02. So, the escape velocity is down by a factor of 7, less than 100 km s-1. Owocki argues that the mass loss of a hot star is set by conditions outside the stellar interior, i.e., opacity in the atmosphere and wind, that results in the radiatively-driven mass loss (Castor et al. 1975). For RSGs, the heavy lifting has already been done by the stellar interior, as a significant fraction of the luminosity of the star has gone into making a bigger radius. "It is kind of like walking with a nearly full glass of water vs a glass that is only 1% full (O star)—even a small jiggle can lead to big changes in the mass loss for a RSG," Owocki concludes.
Finally, let us introduce the Wolf-Rayet stars. These stars have strong emission-line spectra. WR stars come in basically two flavors, WN-type WRs, where the spectrum is dominated by N and He, and WC-type WRs, where the spectrum is dominated by He, C, and O. (A few WO-type WRs have been identified; these are basically WC stars with enhanced O lines.) In the "Conti scenario" (Conti 1976), a massive star peels off its H-rich outer envelope through stellar winds on the main-sequence (perhaps helped by the enhanced mass loss during the LBV phase). Once the H-burning products (N and He) are revealed, the star is spectroscopically identified as a WN-type. Further mass loss eventually peels off these layers, revealing the He-burning products (C and O)
An outstanding question is why the mass-loss rates of WRs are so high; H-poor WRs have derived mass-loss rates about 10× higher than OB stars of the same luminosity. The terminal wind velocities are similar, so it is as if the radiation pressure was somehow more efficient in these H-poor objects. Puls et al. (2008) offers several possibilities, including the speculation that this is due to WR star winds being less "leaky" because the higher core temperature and higher wind density leads to an ionization equilibrium that is stratified. Alternatively, the ionization in the outer winds may be shifted towards lower stages, leading to a more efficient acceleration. Or it could be that WR winds get an extra kick due to the hot ion peak around 160,000 K deep in the WR atmosphere.
What we do know is that the mass-loss rates on the main-sequence depend
upon metallicity, as mentioned earlier, and that therefore it is easier
for a massive star to become a WR at high metallicity than at low. To
put this more precisely,
a 20 M might be able to "peel down" all of the way to a WC star in M31 (where
the metallicity is high, see Table 1), but could
only evolve as far as the WN stage in M33 (where the metallicity is
lower, Table 1). Or perhaps only stars of 60
M
might be able to "peel down" all of the way to a WC star in M31 (where
the metallicity is high, see Table 1), but could
only evolve as far as the WN stage in M33 (where the metallicity is
lower, Table 1). Or perhaps only stars of 60
M and above
can become WRs in the SMC. One expectation then is that the relative
number of RSGs and WRs should be a sensitive function of
metallicity among the galaxies of the Local Group
(Maeder et al. 1980),
with relatively fewer WRs at lower metallicities. In addition, one
expects that the relative number of WC and WN stars should be a strong
function of metallicity, with relatively fewer WCs at lower
metallicities
(Massey & Johnson
1998,
Meynet & Maeder 2005,
Neugent et al. 2012a).
and above
can become WRs in the SMC. One expectation then is that the relative
number of RSGs and WRs should be a sensitive function of
metallicity among the galaxies of the Local Group
(Maeder et al. 1980),
with relatively fewer WRs at lower metallicities. In addition, one
expects that the relative number of WC and WN stars should be a strong
function of metallicity, with relatively fewer WCs at lower
metallicities
(Massey & Johnson
1998,
Meynet & Maeder 2005,
Neugent et al. 2012a).
Massive stars are expected to end their lives as core-collapse SNe,
enriching the interstellar material chemically, and providing a great
deal of mechanical energy. However, the only example we know of this
directly in the Local Group is SN 1987A, where the progenitor star, Sk
-69∘ 202, was known to be a ~
20M B-type supergiant. At the time, evolutionary models did not include a
"blue loop" for such stars; they were supposed to become supernovae as
RSGs.
B-type supergiant. At the time, evolutionary models did not include a
"blue loop" for such stars; they were supposed to become supernovae as
RSGs.
Core-collapse SNe are either hydrogen-rich type II SNe, or hydrogen-poor types Ib and Ic, where the latter are also helium-poor. The type II's are further classified depending upon their light curves (type II-P, whose light curves show a plateau, and II-L, where the light curve shows a magnitude-linear decline in time) or spectral features (IIn, where the spectrum shows narrow emission lines, and IIb, where the spectrum changes to become like that of a Ib).
The lack of hydrogen features in the spectra of types Ib and Ic suggest that the progenitors have been been stripped of their outer hydrogen envelopes. Two prevailing theories for how this stripping occurs are mass-loss through strong stellar winds or through binary interaction. The former naturally associates the Ib/c's with Wolf-Rayet stars, but there are no cases where an actual progenitor of a Ib or Ic has been identified. (Shara et al. 2013 argue that the identification of Wolf-Rayet stars in nearby galaxies serves the additional purpose of identifying Ib/c progenitors, so that when one of these stars explodes we'll be prepared.)
All type II-P core-collapse SNe have long been assumed to come from
RSGs, although the classification
of SN 1987A is that of a (peculiar) II-P and we know it
didn't.
Smartt et al. (2009)
have identified numerous type II-P progenitors in nearby
galaxies as RSGs, as well as summarizing those found by others. They
argue that type II-Ps come from a mass range from 8.5 to 16.5
M . Since
RSGs have masses as large as
25 M
. Since
RSGs have masses as large as
25 M ,
this introduces
the "red supergiant problem": why is the observed upper mass limit
16.5 M
,
this introduces
the "red supergiant problem": why is the observed upper mass limit
16.5 M .
Of course, this mass limit is not directly observed; it is inferred by
making a variety of assumptions not only about the IMF slope
in nearly galaxies, and it also depends upon certain reddening
assumptions, etc.
.
Of course, this mass limit is not directly observed; it is inferred by
making a variety of assumptions not only about the IMF slope
in nearly galaxies, and it also depends upon certain reddening
assumptions, etc.
One of the most remarkable recent astronomical events has been the
explosion (SN 2011dh) of
a YSG in M51 (distance 11 Mpc) as a Type IIb supernova
(Maund et al. 2011).
Two other examples of YSG progenitors for SNe explosions exist; see
Georgy et al. (2013)
and references therein. This fact poses some interesting, but not
insurmountable, challenges
to single-star massive star evolutionary theory (e.g.,
Georgy et al. 2013),
as 15M stars (which is a typical mass for YSGs)
have long been thought to end their lives in the RSG stage.
But significant mass-loss during the RSG may delay the explosion
(Bersten et al. 2012,
Georgy et al. 2013).
Alternatively, these YSGs may have been binaries, and
binary evolution may have played a role in the formation of these SNe.
stars (which is a typical mass for YSGs)
have long been thought to end their lives in the RSG stage.
But significant mass-loss during the RSG may delay the explosion
(Bersten et al. 2012,
Georgy et al. 2013).
Alternatively, these YSGs may have been binaries, and
binary evolution may have played a role in the formation of these SNe.
Of similar import has been the explosion of an LBV in NGC 7259 (distance 25 Mpc, far outside the Local Group), a Type IIn core-collapse supernova (SN); see Mauerhan et al. (2013) and references therein. The star, SN 2009ip, was a transient which had recent eruptions. (In fact, the first such eruption was mistaken for a SN explosion.) As of this writing, the result is still somewhat controversial (see, e.g., Pastorello et al. 2013), but if the discovery is confirmed, it will be remarkable in that for the first time we knew for certain what the progenitor was of a type IIn explosion, and as a demonstration that an LBV could explode as a SN.
1 The mass-loss rates change by 0.01 dex due to temperature from 40,000 to 50,000 K, according to Vink et al. (2000), equation 12. Back.