4.4. The Alfvén theorems

The ideal and resistive MHD descriptions are rather useful in order to illustrate some global properties of the evolution of the plasma which are relevant both in the evolution of large-scale magnetic fields prior to recombination and in the discussion of the gravitational collapse in the presence of magnetic fields. These global properties of the plasma evolution go under the name of Alfvén theorems [87] (see also [88]).

In the ideal limit both the magnetic flux and the magnetic helicity are conserved. This means,

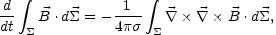(4.24)

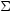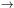
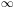where is an arbitrary closed surface which moves with the plasma ⁽¹²⁾. If the expression appearing at the right hand side is sub-leading and the magnetic flux lines evolve glued to the plasma element.

The other quantity which is conserved in the superconducting limit is the magnetic helicity

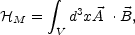(4.25)

where 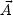is the vector potential whose presence may lead to think that the whole expression (4.25) is not gauge-invariant. In fact ^. is not gauge invariant but, none the less, 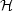_M is gauge-invariant since the integration volume is defined in such a way that the magnetic field 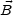is parallel to the surface which bounds V and which we will call 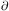V. If 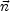is the unit vector normal to 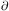V then 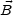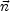^. = 0 on 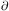V and the gauge dependent contribution to the integral appearing in Eq. (4.25) vanishes. In physical terms the integration may always be performed imagining that the space is sliced in flux tubes of the magnetic field. This procedure is correct provided the magnetic flux is, at least approximately, conserved as implied by Eq. (4.24).

The magnetic gyrotropy

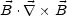(4.26)

it is a gauge invariant measure of the diffusion rate of 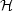_M. In fact, in the resistive approximation [88]

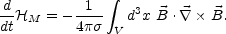(4.27)

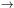
As in the case of Eq. (4.25), for 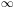the magnetic helicity is approximately constant. The value of the magnetic gyrotropy allows to distinguish different mechanisms for the magnetic field generation. Some mechanisms are able to produce magnetic fields whose flux lines have a non-trivial gyrotropy. The properties of turbulent magnetized plasmas may change depending upon the value of the gyrotropy and of the helicity [87].

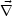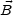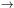
The physical interpretation of the flux and magnetic helicity conservation is the following. In MHD the magnetic field has to be always solenoidal (i.e. ^. = 0). Thus, the magnetic flux conservation implies that, in the superconducting limit (i.e. 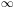) the magnetic flux lines, closed because of the transverse nature of the field, evolve always glued together with the plasma element. In this approximation, as far as the magnetic field evolution is concerned, the plasma is a collection of (closed) flux tubes. The theorem of flux conservation states then that the energetical properties of large-scale magnetic fields are conserved throughout the plasma evolution.

While the flux conservation concerns the energetical properties of the magnetic flux lines, the magnetic helicity concerns chiefly the topological properties of the magnetic flux lines. If the magnetic field is completely stochastic, the magnetic flux lines will be closed loops evolving independently in the plasma and the helicity will vanish. There could be, however, more complicated topological situations [88] where a single magnetic loop is twisted (like some kind of Möbius stripe) or the case where the magnetic loops are connected like the rings of a chain. In both cases the magnetic helicity will not be zero since it measures, essentially, the number of links and twists in the magnetic flux lines. Furthermore, in the superconducting limit, the helicity will not change throughout the time evolution. The conservation of the magnetic flux and of the magnetic helicity is a consequence of the fact that, in ideal MHD, the Ohmic electric field is always orthogonal both to the bulk velocity field and to the magnetic field. In the resistive MHD approximation this is no longer true.

If the conductivity is very large (but finite), the resistive MHD approximation suggests, on one hand, that the magnetic flux is only approximately conserved. On the other hand the approximate conservation of the magnetic helicity implies that the closed magnetic loops may modify their topological structure. The breaking of the flux lines, occurring at finite conductivity, is related to the possibility that bits of magnetic fluxes are ejected from a galaxy into the inter-galactic medium. This phenomenon is called magnetic reconnection and it is the basic mechanism explaining, at least qualitatively, why, during the solar flares, not only charged particles are emitted, but also magnetic fields. In the context of large scale magnetic fields the approximate (or exact) magnetic flux conservation has relevant consequences for the rôle of magnetic fields during gravitational collapse.

¹² Notice that in Ref. [88] Eq. (4.24) has been derived without the 4 term at the right hand side because of different conventions. Back.