


5.1. The standard cosmological model
The standard model of cosmological evolution rests on three important assumptions [100]. The first assumption is that over very large length scales (greater than 50 Mpc) the Universe is described by a homogeneous and isotropic Friedmann-Robertson-Walker (FRW) line element:
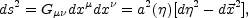 |
(5.1) |
where a( )
is the scale factor and
)
is the scale factor and
 the
conformal-time coordinate (notice that Eq. (5.1) has been written, for
simplicity, in the conformally flat case). The second hypothesis
is that the sources of the evolution of the background geometry are
perfect fluid sources. As a consequence the entropy of the sources is
constant. The third and final hypothesis is that the dynamics of the
sources and of the geometry
is dictated by the general relativistic FRW equations
(16):
the
conformal-time coordinate (notice that Eq. (5.1) has been written, for
simplicity, in the conformally flat case). The second hypothesis
is that the sources of the evolution of the background geometry are
perfect fluid sources. As a consequence the entropy of the sources is
constant. The third and final hypothesis is that the dynamics of the
sources and of the geometry
is dictated by the general relativistic FRW equations
(16):
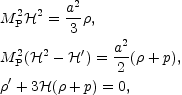 |
(5.2) (5.3) (5.4) |
where 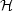 = (ln a)' and the
prime (17) denotes the
derivation with
respect to
= (ln a)' and the
prime (17) denotes the
derivation with
respect to  . Recall also, for notational convenience, that
aH =
. Recall also, for notational convenience, that
aH = 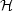 where
H =
where
H = 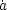 / a
is the conventional Hubble parameter.
The various tests of the standard cosmological model are well known
[101,
102].
Probably one of the most stringent one comes from the possible
distortions, in the Rayleigh-Jeans region, of the CMB spectrum. The
absence of these distortions clearly rules out steady-state cosmological
models. In the standard cosmological model
one usually defines the proper distance of the event horizon at the time
t1
/ a
is the conventional Hubble parameter.
The various tests of the standard cosmological model are well known
[101,
102].
Probably one of the most stringent one comes from the possible
distortions, in the Rayleigh-Jeans region, of the CMB spectrum. The
absence of these distortions clearly rules out steady-state cosmological
models. In the standard cosmological model
one usually defines the proper distance of the event horizon at the time
t1
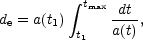 |
(5.5) |
this distance represents the maximal extension of the region over which causal connection is possible. Furthermore, the proper distance of the particle horizon can also be defined:
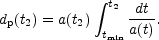 |
(5.6) |
If the scale factor is parametrized as a(t) ~
t , for
0 <
, for
0 <  < 1 the
Universe experiences a decelerated expansion, i.e.
< 1 the
Universe experiences a decelerated expansion, i.e.
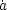 > 0 and
> 0 and
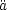 < 0 while the
curvature scale decreases, i.e.
< 0 while the
curvature scale decreases, i.e.
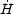 < 0. This is the
peculiar
behaviour when the fluid sources are dominated either by dust (p
= 0) or by radiation (p =
< 0. This is the
peculiar
behaviour when the fluid sources are dominated either by dust (p
= 0) or by radiation (p =
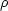 / 3).
In the case of the standard model, the particle horizon increases
linearly in cosmic time (therefore faster than the scale factor). This
implies that the CMB radiation, today observed with a temperature
of 2.7K over the whole present horizon has been emitted from
space-time regions which were not in causal contact. This problem is
known as the horizon problem of the
standard cosmological model. The other problem of the standard model
is related to the fact that today the intrinsic (spatial) curvature
k / a2 is smaller than the extrinsic
curvature, i.e. H2. Recalling that
k / (a2 H2) = k /
/ 3).
In the case of the standard model, the particle horizon increases
linearly in cosmic time (therefore faster than the scale factor). This
implies that the CMB radiation, today observed with a temperature
of 2.7K over the whole present horizon has been emitted from
space-time regions which were not in causal contact. This problem is
known as the horizon problem of the
standard cosmological model. The other problem of the standard model
is related to the fact that today the intrinsic (spatial) curvature
k / a2 is smaller than the extrinsic
curvature, i.e. H2. Recalling that
k / (a2 H2) = k /
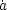 2 it is clear
that if
2 it is clear
that if 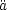 < 0,
1 /
< 0,
1 / 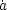 2
increases so that the intrinsic curvature could be, today, arbitrarily
large. The third problem of the standard cosmological model is related
to the generation of the large entropy of the present Universe.
The solution of the kinematical problems of the standard model is
usually discussed in the framework of a phase of accelerated expansion
[103],
i.e.
2
increases so that the intrinsic curvature could be, today, arbitrarily
large. The third problem of the standard cosmological model is related
to the generation of the large entropy of the present Universe.
The solution of the kinematical problems of the standard model is
usually discussed in the framework of a phase of accelerated expansion
[103],
i.e. 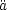 > 0 and
> 0 and
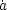 > 0. In the case
of inflationary dynamics the extension of the causally connected regions
grows as the scale factor and hence faster than in the decelerated
phase. This solves the horizon problem. Furthermore, during inflation
the contribution of the spatial curvature becomes very small. The way
inflation solves the curvature problem is by producing a very tiny
spatial curvature at the onset of the radiation epoch taking
place right after inflation. The spatial curvature can well grow during
the decelerated phase of expansion but is will be always subleading
provided inflation lasted for sufficiently long time. In fact, the
minimal requirement in order to solve these
problems is that inflation lasts, at least, 60-efolds.
The final quantity which has to be introduced is the Hubble radius
H-1(t). This quantity is local in time,
however, a sloppy nomenclature often exchanges the Hubble radius with
the horizon. Since this terminology is rather common, it will also be
used here. In the following applications it will be relevant to recall
some of the useful thermodynamical relations.
In particular, in radiation dominated Universe, the relation between the
Hubble parameter and the temperature is given by
> 0. In the case
of inflationary dynamics the extension of the causally connected regions
grows as the scale factor and hence faster than in the decelerated
phase. This solves the horizon problem. Furthermore, during inflation
the contribution of the spatial curvature becomes very small. The way
inflation solves the curvature problem is by producing a very tiny
spatial curvature at the onset of the radiation epoch taking
place right after inflation. The spatial curvature can well grow during
the decelerated phase of expansion but is will be always subleading
provided inflation lasted for sufficiently long time. In fact, the
minimal requirement in order to solve these
problems is that inflation lasts, at least, 60-efolds.
The final quantity which has to be introduced is the Hubble radius
H-1(t). This quantity is local in time,
however, a sloppy nomenclature often exchanges the Hubble radius with
the horizon. Since this terminology is rather common, it will also be
used here. In the following applications it will be relevant to recall
some of the useful thermodynamical relations.
In particular, in radiation dominated Universe, the relation between the
Hubble parameter and the temperature is given by
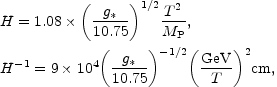 |
(5.7) |
where g* is the effective number of
relativistic degrees of freedom
at the corresponding temperature. Eq. (5.2), implying
H2 MP2 =
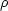 / 3, has been
used in Eq. (5.7) together with the known relations valid in a radiation
dominated background
/ 3, has been
used in Eq. (5.7) together with the known relations valid in a radiation
dominated background
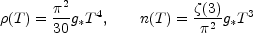 |
(5.8) |
where 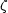 (3)
(3)
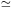 1.2.
In Eq. 5.8) the thermodynamical relation for the
number density n(T) has been also introduced for future
convenience.
1.2.
In Eq. 5.8) the thermodynamical relation for the
number density n(T) has been also introduced for future
convenience.
5.1.1. Inflationary dynamics and its extensions
The inflationary dynamics can be realized in different ways. Conventional inflationary models are based either on one single inflaton field [104, 105, 106, 107] or on various fields [108] (see [109] for a review). Furthermore, in the context of single-field inflationary models one oughts to distinguish between small-field models [106] (like in the so-called new-inflationary models) and large-field models [107] (like in the case of chaotic models).
In spite of their various quantitative differences, conventional inflationary models are based on the idea that during the phase of accelerated expansion the curvature scale is approximately constant (or slightly decreasing). After inflation, the radiation dominated phase starts. It is sometimes useful for numerical estimates to assume that radiation suddenly dominates at the end of inflation. In this case the scale factor can be written as
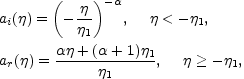 |
(5.9) |
where  is some effective
exponent parameterizing the dynamics
of the primordial phase of the Universe. Notice that if
is some effective
exponent parameterizing the dynamics
of the primordial phase of the Universe. Notice that if
 = 1
we have that the primordial phase coincides with a de Sitter
inflationary epoch. The case
= 1
we have that the primordial phase coincides with a de Sitter
inflationary epoch. The case
 = 1 is not completely
realistic since
it corresponds to the case where the energy-momentum tensor
is simply given by a (constant) cosmological term. In this case
the scalar fluctuations of the geometry are not amplified and the
large-scale angular anisotropy in the CMB would not be reproduced.
The idea is then to discuss more realistic energy-momentum tensors
leading to a dynamical behaviour close to the one of pure de Sitter
space, hence the name quasi-de Sitter space-times. Quasi-de Sitter
dynamics can be realized in different ways. One possibility is to
demand that the inflaton slowly rolls down from its potential
obeying the approximate equations
= 1 is not completely
realistic since
it corresponds to the case where the energy-momentum tensor
is simply given by a (constant) cosmological term. In this case
the scalar fluctuations of the geometry are not amplified and the
large-scale angular anisotropy in the CMB would not be reproduced.
The idea is then to discuss more realistic energy-momentum tensors
leading to a dynamical behaviour close to the one of pure de Sitter
space, hence the name quasi-de Sitter space-times. Quasi-de Sitter
dynamics can be realized in different ways. One possibility is to
demand that the inflaton slowly rolls down from its potential
obeying the approximate equations
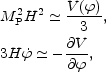 |
(5.10) |
valid provided
 1 =
-
1 =
- 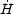 /
H2 << 1 and
/
H2 << 1 and
 2 =
2 =
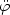 / (H
/ (H
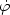 )
<< 1. There also exist
exact inflationary solutions like the power-law solutions obtainable in
the case of exponential potentials:
)
<< 1. There also exist
exact inflationary solutions like the power-law solutions obtainable in
the case of exponential potentials:
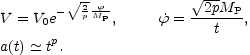 |
(5.11) |
Since, from the exact equations, 2MP2
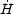 =
-
=
-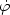 2 the two slow-roll parameters can also be
written as
2 the two slow-roll parameters can also be
written as
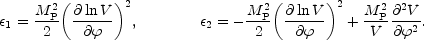 |
(5.12) |
In the case of the exponential potential (5.11)
the slow-roll parameters are all equal,
 1 =
1 =
 2 = 1 /
p. Typical potentials leading to the usual inflationary dynamics
are power-law potentials of the type
V(
2 = 1 /
p. Typical potentials leading to the usual inflationary dynamics
are power-law potentials of the type
V(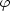 )
)
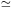
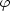 n,
exponential potentials, trigonometric potentials and nearly any
potential satisfying, in some
region of the parameter space, the slow-roll conditions.
n,
exponential potentials, trigonometric potentials and nearly any
potential satisfying, in some
region of the parameter space, the slow-roll conditions.
Inflation can also be realized in the case when the curvature scale is
increasing, i.e. 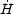 > 0
and
> 0
and 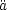 > 0.
This is the case of superinflationary dynamics. For instance the
propagation of fundamental strings in curved backgrounds
[110,
111]
may lead to superinflationary solutions
[113,
114].
A particularly simple case of superinflationary solutions arises in the
case when internal dimensions are present.
> 0.
This is the case of superinflationary dynamics. For instance the
propagation of fundamental strings in curved backgrounds
[110,
111]
may lead to superinflationary solutions
[113,
114].
A particularly simple case of superinflationary solutions arises in the
case when internal dimensions are present.
Consider a homogeneous and anisotropic manifold whose line element can be written as
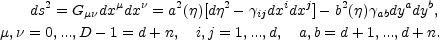 |
(5.13) |
[ is the
conformal time coordinate related, as usual to the cosmic time
t =
is the
conformal time coordinate related, as usual to the cosmic time
t = 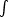 a(
a( )
d
)
d ;
;
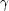 ij(x),
ij(x),
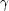 ab(y) are the metric
tensors of two maximally symmetric Euclidean manifolds parameterized,
respectively, by the "internal" and the "external" coordinates
{xi} and {ya}].
The metric of Eq. (5.13) describes the situation in which the d
external dimensions (evolving with scale factor
a(
ab(y) are the metric
tensors of two maximally symmetric Euclidean manifolds parameterized,
respectively, by the "internal" and the "external" coordinates
{xi} and {ya}].
The metric of Eq. (5.13) describes the situation in which the d
external dimensions (evolving with scale factor
a( )) and
the n internal ones (evolving with scale factor
b(
)) and
the n internal ones (evolving with scale factor
b( ))
are dynamically decoupled from each other
[115].
))
are dynamically decoupled from each other
[115].
A model of background evolution can be generically written as
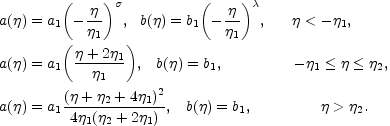 |
(5.14) |
In the parameterization of Eq. (5.14)
the internal dimensions grow (in conformal time) for
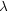 < 0 and they
shrink for
< 0 and they
shrink for
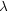 > 0
(18).
> 0
(18).
Superinflationary solutions are also common in the context
of the low-energy string effective action
[119,
120,
121].
In critical superstring theory the electromagnetic field
Fµ is
coupled not only to the metric
(gµ
is
coupled not only to the metric
(gµ ),
but also to the dilaton background
(
),
but also to the dilaton background
(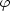 ).
In the low energy limit such interaction is represented by the
string effective action
[119,
120,
121],
which reads, after reduction from ten to four expanding dimensions,
).
In the low energy limit such interaction is represented by the
string effective action
[119,
120,
121],
which reads, after reduction from ten to four expanding dimensions,
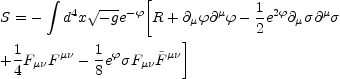 |
(5.15) |
were 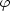 =
=
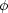 - ln
V6
- ln
V6  ln(g2) controls the
tree-level four-dimensional gauge coupling
(
ln(g2) controls the
tree-level four-dimensional gauge coupling
(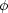 being the
ten-dimensional dilaton field, and V6 the volume of the
six-dimensional compact internal space). The field
being the
ten-dimensional dilaton field, and V6 the volume of the
six-dimensional compact internal space). The field
 is the Kalb-Ramond axion
whose pseudoscalar coupling to the gauge fields may also be interesting.
is the Kalb-Ramond axion
whose pseudoscalar coupling to the gauge fields may also be interesting.
In the inflationary models based on the above effective action
[122,
123]
the dilaton background is not at all constant, but
undergoes an accelerated evolution from the string perturbative vacuum
(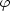 =
-
=
- 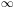 ) towards the strong
coupling regime, where it is expected to remain frozen at its
present value. The peculiar feature of this string cosmological scenario
(sometimes called pre-big bang
[123])
is that not only the curvature evolves but also the gauge
coupling. Suppose, for the moment that the gauge fields are set to zero.
The phase
of growing curvature and dilaton coupling
(<
) towards the strong
coupling regime, where it is expected to remain frozen at its
present value. The peculiar feature of this string cosmological scenario
(sometimes called pre-big bang
[123])
is that not only the curvature evolves but also the gauge
coupling. Suppose, for the moment that the gauge fields are set to zero.
The phase
of growing curvature and dilaton coupling
(<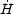 > 0,
> 0,
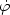 > 0), driven by the kinetic energy of the dilaton field, is
correctly described in terms of the lowest order string effective
action only up to the conformal time
> 0), driven by the kinetic energy of the dilaton field, is
correctly described in terms of the lowest order string effective
action only up to the conformal time
 =
=
 s at
which the curvature reaches the string scale Hs =
s at
which the curvature reaches the string scale Hs =
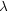 s-1
(
s-1
(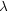 s
s
 (
( ')1/2
is the fundamental length of string theory).
A first important parameter of this cosmological model is thus the value
')1/2
is the fundamental length of string theory).
A first important parameter of this cosmological model is thus the value
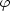 s
attained by the dilaton at
s
attained by the dilaton at
 =
=
 s.
Provided such value is sufficiently negative (i.e. provided the coupling
g = e
s.
Provided such value is sufficiently negative (i.e. provided the coupling
g = e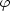 /2 is sufficiently small to be still in the
perturbative region at
/2 is sufficiently small to be still in the
perturbative region at
 =
=
 s),
it is also arbitrary, since there
is no perturbative potential to break invariance under shifts of
s),
it is also arbitrary, since there
is no perturbative potential to break invariance under shifts of
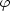 .
For
.
For  >
>
 s
high-derivatives terms (higher orders in
s
high-derivatives terms (higher orders in
 ')
become important in the string effective action,
and the background enters a genuinely "stringy" phase of
unknown duration. An assumption of string cosmology
is that the stringy phase eventually ends at some conformal time
')
become important in the string effective action,
and the background enters a genuinely "stringy" phase of
unknown duration. An assumption of string cosmology
is that the stringy phase eventually ends at some conformal time
 1
in the strong coupling regime. At this time the dilaton,
feeling a non-trivial potential, freezes to its present constant
value
1
in the strong coupling regime. At this time the dilaton,
feeling a non-trivial potential, freezes to its present constant
value 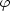 =
=
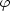 1
and the standard radiation-dominated era starts. The total duration
1
and the standard radiation-dominated era starts. The total duration
 1 /
1 /
 s,
or the total red-shift zs
encountered during the stringy epoch (i.e. between
s,
or the total red-shift zs
encountered during the stringy epoch (i.e. between
 s and
s and
 1),
will be the second crucial parameter besides
1),
will be the second crucial parameter besides
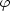 s
entering our discussion. For the purpose of this paper, two
parameters are enough to specify completely our model of
background, if we accept that during the string phase the
curvature stays controlled by the string scale, that is
H
s
entering our discussion. For the purpose of this paper, two
parameters are enough to specify completely our model of
background, if we accept that during the string phase the
curvature stays controlled by the string scale, that is
H 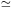 g
MP
g
MP 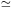
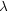 s-1 (Mp is the
Planck mass) for
s-1 (Mp is the
Planck mass) for
 s
<
s
<  <
<
 1.
1.
During the string era
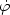 and H are approximately constant, while, during the
dilaton-driven epoch
and H are approximately constant, while, during the
dilaton-driven epoch
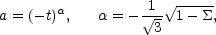 |
(5.16) |
Here 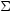

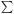 i
i
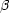 i2 represents the
possible effect of internal dimensions whose radii bi
shrink like (- t)
i2 represents the
possible effect of internal dimensions whose radii bi
shrink like (- t)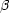 i for
t
i for
t
0- (for the sake of definiteness we show in the figure the case
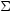 = 0).
The shape of the coupling curve corresponds to the fact that the
dilaton is constant during the radiation era, that
= 0).
The shape of the coupling curve corresponds to the fact that the
dilaton is constant during the radiation era, that
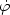 is
approximately constant during the string era, and that it evolves
like
is
approximately constant during the string era, and that it evolves
like
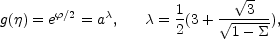 |
(5.17) |
during the dilaton-driven era.
An interesting possibility, in the pre-big bang context is that the exit to the phase of decelerated expansion and decreasing curvature takes place without any string tension correction. Recently a model of this kind has been proposed [124]. The idea consists in adding a non-local dilaton potential which is invariant under scale factor duality. The evolution equations of the metric and of the dilaton will then become, in 4 space-time dimensions,
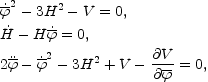 |
(5.18) |
where 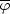 =
=
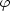 - 3 log
a is the shifted dilaton.
A particular solution to these equations will be given by
- 3 log
a is the shifted dilaton.
A particular solution to these equations will be given by
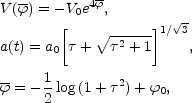 |
(5.19) (5.20) (5.21) |
where
 |
(5.22) |
This solution interpolates smoothly between two self-dual solutions. For
t 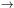 -
-  the background
superinflates while for
t
the background
superinflates while for
t  +
+
 the
decelerated FRW limit is recovered.
the
decelerated FRW limit is recovered.
16 Units
MP = (8 G)-1/2 = 1.72 × 1018 GeV will be used.
Back.
G)-1/2 = 1.72 × 1018 GeV will be used.
Back.
17 The overdot will usually denote
derivation with respect to the cosmic time coordinate t related
to conformal time as dt =
a( )
d
)
d .
Back.
.
Back.
18 To assume that the internal
dimensions are constant during the
radiation and matter dominated epoch is not strictly necessary. If
the internal dimensions have a time variation during the radiation
phase we must anyway impose the BBN bounds on their variation
[116,
117,
118].
The tiny variation allowed by BBN implies that
b( ) must be
effectively constant for practical purposes.
Back.
) must be
effectively constant for practical purposes.
Back.