A. COMPLEMENTS ON MHD DESCRIPTION

Two fluids and one-fluid MHD equations

In a two-fluid plasma description the charge carriers are the ions (for simplicity we can think of them as protons) and the electrons. The two fluid equations treat the ions and the electrons as two conducting fluids which are coupled as in Eqs. (4.8)-(4.12). Given the two- fluid description, one-fluid variables can be defined directly in terms of the two-fluid variables

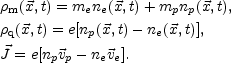(A.1)

In the case of a globally neutral plasma n_e ~ n_p = n_q and 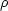_q = 0. The ion and electron equations then become

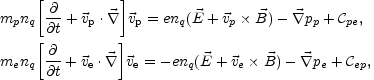(A.2) (A.3)

where 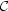_pe and 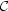_pe are the collision terms. In the globally neutral case the center of mass velocity becomes

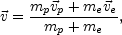(A.4)

and the one-fluid mass and charge density conservations become

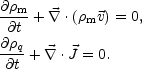(A.5) (A.6)

Summing up Eqs. (A.2) and (A.3) leads, with some algebra involving the continuity equation, to the momentum transport equation in the one-fluid theory:

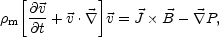(A.7)

where P = P_e + P_i. In Eq. (A.7) the collision term vanishes if there are no neutral particles, i.e. if the plasma is fully ionized. The final equation of the one-fluid description is obtained by taking the difference of Eqs. (A.2) and (A.3) after having multiplied Eq. (A.2) by m_e and Eq. (A.3) by m_p. This procedure is more tricky and it is discussed in standard textbooks of plasma physics [85, 86]. The key points in the derivation are that the limit for m_e / m_p 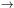0 must be taken. The problem with this procedure is that the subtraction of the two mentioned equations does not guarantee that viscous and collisional effects are negligible. The result of this procedure is the so-called one-fluid generalized Ohm law:

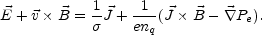(A.8)

The term 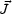× B is nothing but the Hall current and 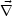P_e is often called thermoelectric term. Finally the term 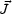/ is the resistivity term and is the conductivity of the one-fluid description. In Eq. (A.8) the pressure has been taken to be isotropic. This is, however, not a direct consequence of the calculation presented in this Appendix but it is an assumption which may (and should) be relaxed in some cases. In the plasma physics literature [85, 86] the anisotropic pressure contribution is neglected for the simple reason that experiments terrestrial plasmas show that this terms is often negligible.

Conservation laws in resistive MHD

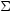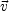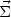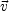Consider and arbitrary closed surface which moves with the plasma. Then, by definition of the bulk velocity of the plasma ( we can also write d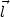 = × d d. The (total) time derivative of the flux can therefore be expressed as

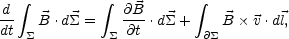(A.9)

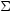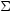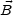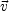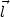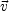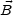where is the boundary of . Using now the properties of the vector products (i.e. × ^. d = - × ^. d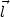) we can express 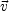× 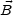though the Ohm law given in Eq. (4.23) and we obtain that

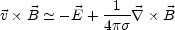(A.10)

Using now Eq. (A.9) together with the Stokes theorem, the following expression can be obtained

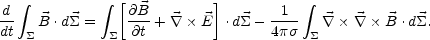(A.11)

From the Maxwell's equations the first part at the right hand side of Eq. (A.11) is zero and Eq. (4.24), expressing the Alfvén theorem, is recovered.

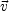
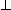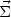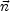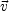
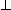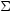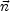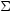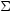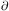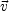
With similar algebraic manipulations (involving the use of various vector identities), the conservation of the magnetic helicity can be displayed. Consider a closed volume in the plasma, then we can write that dV = d³ x = ^. d d ^. d d where is the unit vector normal to (the boundary of V, i.e. = V) and 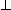is the component of the bulk velocity orthogonal to 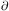V. The (total) time derivative of the magnetic helicity can now be written as

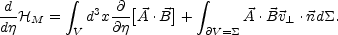(A.12)

The partial derivative at the right hand side of Eq. (A.12) can be made explicit. Then the one-fluid MHD equations should be used recalling that the relation between the electromagnetic fields and the vector potential, for instance in the Coulomb gauge. Finally using again the Ohm law and transforming the obtained surface integrals into volume integrals (through the divergence theorem) Eq. (4.27), expressing the conservation of the helicity, can be obtained.

In spite of the fact that the conservation of the magnetic helicity can be derived in a specific gauge, the magnetic helicity is indeed a gauge invariant quantity. Consider a gauge transformation

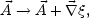(A.13)

then the magnetic helicity changes as

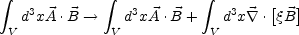(A.14)

(in the second term at the right hand side we used the fact that the magnetic field is divergence free). By now using the divergence theorem we can express the volume integral as

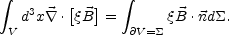(A.15)

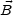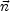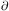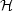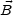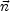Now if, as we required, ^. = 0 in V, the integral is exactly zero and _M is gauge invariant. The condition ^. = 0 is not specific of a particular profile of the magnetic field. It can be always achieved by slicing the volume of integration in small flux tubes where, by definition, the magnetic field is orthogonal to the walls of the flux tube.