


2.4. Including Curvature
It is true that we know observationally that the universe today is flat
to a high degree of accuracy. However, it is instructive, and useful
when considering early cosmology, to consider how the solutions we have
already identified change when curvature is included. Since we include
this mainly for illustration we will focus on the separate cases of
dust-filled and radiation-filled FRW models with zero cosmological
constant. This calculation is an example of one that is made much easier
by working in terms of conformal time
 .
.
Let us first consider models in which the energy density is dominated by matter (w = 0). In terms of conformal time the Einstein equations become
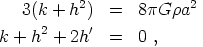 |
(38) |
where a prime denotes a derivative with respect to conformal time and
h( )
)
 a' /
a. These equations are then easily solved for
h(
a' /
a. These equations are then easily solved for
h( ) giving
) giving
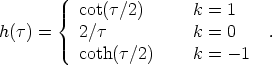 |
(39) |
This then yields
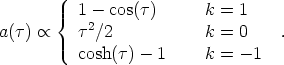 |
(40) |
One may use this to derive the connection between cosmic time and conformal time, which here is
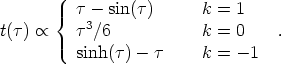 |
(41) |
Next we consider models dominated by radiation (w = 1/3). In terms of conformal time the Einstein equations become
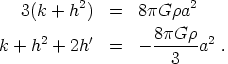 |
(42) |
Solving as we did above yields
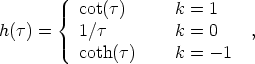 |
(43) |
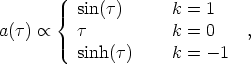 |
(44) |
and
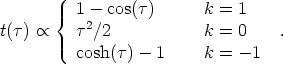 |
(45) |
It is straightforward to interpret these solutions by examining the
behavior of the scale factor
a( ); the qualitative
features are
the same for matter- or radiation-domination. In both cases, the
universes with positive curvature (k = + 1) expand from an initial
singularity with a = 0, and later recollapse again. The initial
singularity is the Big Bang, while the final singularity is sometimes
called the Big Crunch. The universes
with zero or negative curvature begin at the Big Bang and
expand forever. This behavior is
not inevitable, however; we will see below how it can be altered by
the presence of vacuum energy.
); the qualitative
features are
the same for matter- or radiation-domination. In both cases, the
universes with positive curvature (k = + 1) expand from an initial
singularity with a = 0, and later recollapse again. The initial
singularity is the Big Bang, while the final singularity is sometimes
called the Big Crunch. The universes
with zero or negative curvature begin at the Big Bang and
expand forever. This behavior is
not inevitable, however; we will see below how it can be altered by
the presence of vacuum energy.