


3.3.8. Core Profiles
This review of elliptical-ga1axy brightness profiles has so far been based on arbitrary analytic fitting functions and departures from them. The reason for this is that we have no secure model of the profile shape in the absence of an understanding of the velocity anisotropies. This is less true in galaxy cores. It is not implausible that violent relaxation may have produced cores that are isothermal (e.g., King 1966, 1978). However, this may be an oversimplification (1) if there exist large nuclear mass concentrations such as black holes, or (2) if the dynamics of galaxy formation were sufficiently complicated. For example, cores could be triaxial (Schwarzschild 1980a; Binney 1980a, 1981b, 1982a), as observed in the nucleus of M31 (see below). There has been no systematic study of core shapes or velocity anisotropies. I wish to note this important problem, but will not discuss it further. I will review recent work on the brightness profiles of cores, which shows that only some of them are isothermal. The rest have non-zero brightness gradients near the center, an effect which may indicate the presence of a nuclear "black hole", but which can also be interpreted in other ways. As emphasized by Schweizer (1979, 1981a) and others, atmospheric seeing has a major impact on our ability to detect and interpret interesting features in galaxy cores. This problem will also be discussed in detail. Previous reviews on cores have been published by Faber (1980) and by Illingworth (1980).
Examples of isothermals fitted to galaxy profiles are given in
Figure 19. The upper two galaxies are among the
very few
(Schweizer 1979)
in which the cores are large enough that seeing is not a major
factor. NGC 4472 is well described by an isothermal.
NGC 4636 is not
isothermal unless there are large errors in the photometry. (The
King 1978
data are the best photographic photometry of cores in the literature,
but they need to be verified using, e.g., a CCD.) Many galaxies
with smaller cores are well described by seeing-convolved isothermals;
Figure 19 gives two examples. If this simplest
interpretation of the
profiles is correct, then seeing corrections to the parameters are
small enough to be practical (see also Fig. 21).
However, in many
galaxies an isothermal is a good fit only in an unphysically small
radius range (i.e.,
r  rc). The approximate core radius may still be
a useful parameter for these galaxies, but the deviations are
physically interesting and need to be explained. These deviations are
largest in NGC 4636 and in M87
(Young et al. 1978a)
and progressively
smaller in NGC 4589, 4406, 4621, 4697, 4382, 5846 and 7626. (The last
three galaxies are not ranked; cf.
King 1978
for a similar ranking.
The "isothermal" galaxies are NGC 2300, 3379, 4261, 4365, 4374, 4472,
4552, 4649 and 6703.) If there are signs of these deviations in half
of the galaxies studied, how compelling is an isothermal model? In
particular
(Schweizer 1979),
how much extra light can be hidden in the
nucleus of even an apparently isothermal galaxy? This question
motivates a detailed examination of seeing effects, following
Schweizer (1979,
1981a;
see also
de Vaucouleurs 1979,
and references therein).
The results are still somewhat ambiguous and model-dependent. However,
it is clear that interesting amounts of light can be hidden in the
nuclei of most galaxies, even many which appear isothermal.
rc). The approximate core radius may still be
a useful parameter for these galaxies, but the deviations are
physically interesting and need to be explained. These deviations are
largest in NGC 4636 and in M87
(Young et al. 1978a)
and progressively
smaller in NGC 4589, 4406, 4621, 4697, 4382, 5846 and 7626. (The last
three galaxies are not ranked; cf.
King 1978
for a similar ranking.
The "isothermal" galaxies are NGC 2300, 3379, 4261, 4365, 4374, 4472,
4552, 4649 and 6703.) If there are signs of these deviations in half
of the galaxies studied, how compelling is an isothermal model? In
particular
(Schweizer 1979),
how much extra light can be hidden in the
nucleus of even an apparently isothermal galaxy? This question
motivates a detailed examination of seeing effects, following
Schweizer (1979,
1981a;
see also
de Vaucouleurs 1979,
and references therein).
The results are still somewhat ambiguous and model-dependent. However,
it is clear that interesting amounts of light can be hidden in the
nuclei of most galaxies, even many which appear isothermal.
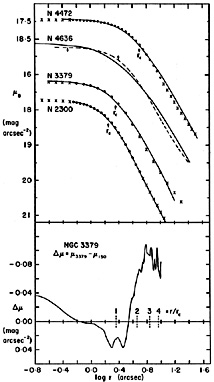 | |||
Figure 19. Fits of seeing-convolved
isothermal core models to
profiles (solid lines) of four elliptical galaxies. The profiles of
NGC 4472, 4636 and 2300 are from
King (1978);
that of NGC 3379 is from
Kormendy (1977a, see
de Vaucouleurs and
Capaccioli 1979,
Appendix I).
Model points shown as filled circles were used in the least-squares
fits; points not used are shown as crosses. The model profiles are
isothermals (log rt / rc =
| |||
| NGC 4472: | rc = 5.0"; | rc, app = 5.5"; |
 * =
0.85". * =
0.85". |
| NGC 4636: | rc = 3.0"; | rc, app = 3.2"; |
 * =
0.58". * =
0.58". |
| NGC 3379: | rc = 2.3"; | rc, app = 2.9"; |  * = 0.88". * = 0.88". |
| NGC 2300: | rc = 1.8"; | rc, app = 2.1"; |  * = 0.67". * = 0.67". |
Here rc, app is the apparent core radius ignoring seeing and rc the true core radius of the fit illustrated. The lower panel shows the deviations of the fit in more detail for NGC 3379. At the center the galaxy is brighter than the model by 0.04 mag arcsec-2. Thus there is no significant evidence for peculiarities such as a central mass concentration or black hole, as suggested by de Vaucouleurs and Capaccioli (1979). A preferable interpretation seems to be that the center is well described by an isothermal, the profile from 17-21 B mag arcsec-2 by an r1/4 law with normal parameters, and the outer profile by the usual tidal distension for a T3 galaxy (Fig. 14). | |||
The nearest, best-studied nucleus is that of M31. In Stratoscope II observations
(Light, Danielson and
Schwarzschild 1974)
this is a
clearly resolved feature rising above the core profile of the bulge
(rc  19", central surface brightness
µ0 ~ 17.0 B mag arcsec-2). The
diameter of the nucleus at half of central intensity is
1.0" × 1.6", the
central surface brightness is 13.7 ± 0.3 B mag
arcsec-2. These values
are corrected for an instrumental point-spread function with a dispersion
19", central surface brightness
µ0 ~ 17.0 B mag arcsec-2). The
diameter of the nucleus at half of central intensity is
1.0" × 1.6", the
central surface brightness is 13.7 ± 0.3 B mag
arcsec-2. These values
are corrected for an instrumental point-spread function with a dispersion
 *
*
 0.1". The total
apparent B magnitude is 13.6 ± 0.3. Other
parameters will be given below in Table 3. There
are a number of
reasons for believing that the nucleus and bulge of M31 are dynamically distinct entities (e.g.,
Schwarzschild 1980a;
Tremaine and Ostriker
1982).
(1) Schwarzschild
(1980a)
and Light et al. (1974)
note that
the brightness distribution is suggestive of separate components. For
example, there is an isophote twist of ~ 20° between the
nucleus and
bulge, indicating that these features are differently triaxial. (2)
The rotation curve of M31 has a sharp peak of amplitude V ~ 100 km
s-1 at r
0.1". The total
apparent B magnitude is 13.6 ± 0.3. Other
parameters will be given below in Table 3. There
are a number of
reasons for believing that the nucleus and bulge of M31 are dynamically distinct entities (e.g.,
Schwarzschild 1980a;
Tremaine and Ostriker
1982).
(1) Schwarzschild
(1980a)
and Light et al. (1974)
note that
the brightness distribution is suggestive of separate components. For
example, there is an isophote twist of ~ 20° between the
nucleus and
bulge, indicating that these features are differently triaxial. (2)
The rotation curve of M31 has a sharp peak of amplitude V ~ 100 km
s-1 at r
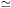 2". At larger
radii V decreases to ~ 20 km s-1, before beginning
to rise again in the bulge
(Lallemand, Duchesne
and Walker 1960;
Morton and Thuan 1973;
Walker 1974;
Peterson 1978a;
McElroy 1981).
This suggests the presence of two mass components of very different
characteristic radii. (3) There are indications of spectral
differences between the bulge and the nucleus; these would imply
population or metallicity differences (e.g.,
Cohen 1979;
Faber and French 1980,
but see
Persson et al. 1980).
(4) Whitmore (1980)
suggests that the velocity dispersion
2". At larger
radii V decreases to ~ 20 km s-1, before beginning
to rise again in the bulge
(Lallemand, Duchesne
and Walker 1960;
Morton and Thuan 1973;
Walker 1974;
Peterson 1978a;
McElroy 1981).
This suggests the presence of two mass components of very different
characteristic radii. (3) There are indications of spectral
differences between the bulge and the nucleus; these would imply
population or metallicity differences (e.g.,
Cohen 1979;
Faber and French 1980,
but see
Persson et al. 1980).
(4) Whitmore (1980)
suggests that the velocity dispersion
 n of the
nucleus may be larger than the central dispersion
n of the
nucleus may be larger than the central dispersion
 0 of the bulge:
0 of the bulge:
 0 /
0 /
 n = 0.83
± 0.12. (5)
Tremaine and Ostriker
(1982)
have shown that the dynamical effects of the bulge
and the nucleus on each other are small. They derive dynamical models
for the nucleus, and discuss constraints on its origin in some detail.
Although the precise nature of the nucleus is not yet understood, it is
unlikely to be the direct response of a stellar system to a nuclear
"black hole". Tremaine and Ostriker conclude that the nucleus is a
system of relatively ordinary stars on almost radial orbits.
n = 0.83
± 0.12. (5)
Tremaine and Ostriker
(1982)
have shown that the dynamical effects of the bulge
and the nucleus on each other are small. They derive dynamical models
for the nucleus, and discuss constraints on its origin in some detail.
Although the precise nature of the nucleus is not yet understood, it is
unlikely to be the direct response of a stellar system to a nuclear
"black hole". Tremaine and Ostriker conclude that the nucleus is a
system of relatively ordinary stars on almost radial orbits.
Are there similar nuclei in elliptical galaxies? Schweizer (1979) argues that this is probable, basically by analogy with M31 and M32. This analogy is not very secure, because M31 and M32 are much less luminous than typical ellipticals studied to date (the absolute magnitude of the bulge of M31 is only MB ~ -18.6, Kormendy and Illingworth 1982a, and M32 is much fainter still). Also, observed differences between bulges and bright ellipticals are suggestive of dynamical differences (sections 3.4.1; 4.2.6). However, Schweizer (1979) notes quite correctly that if M31 were placed at the typical distance of ellipticals studied to date, i.e., in the Virgo cluster, the nucleus would not be detected in ground-based measurements.
To determine how much nuclear light could be hidden in
King's (1978)
photometry, Schweizer adopts the computational convenience of
r1/4 laws. These model a particular amount of nuclear
cusp in an
arbitrary but plausible way, since they just extrapolate the overall
profile to the center. (In fact, the nucleus and bulge of M31 have a
combined profile which is approximately as bright at the center as the
r1/4 law of the bulge.) Schweizer shows that when
r1/4 laws are
convolved with realistic point-spread functions, artificial cores are
generated whose apparent radii
rc, app depend on the effective radii
and the stellar seeing
 *.
As Figure 20 shows, only a few of
King's galaxies have observed core radii which are much larger than
these false core radii. That is, M87, NGC 4649 and NGC 4472 are well
resolved, and NGC 4365 and 4636 are reasonably well resolved. Little
extra light can be hidden in the nuclei of these galaxies. And,
indeed, M87 did not successfully hide its core peculiarities
from
Young et al. (1978a),
nor does NGC 4636 appear isothermal in
Figure 19.
On the other hand, most galaxies in
Figure 20 fall close to the lines
describing the false cores. This means that their cores are not resolved
unambiguously. These galaxies could have isothermal cores, as illustrated
in Figure 19. However they could instead be
hiding nuclear brightness cusps as strong as those in
r1/4 laws. Furthermore, in at least one case where an
isothermal is a poor fit, a convolved r1/4
law gives an excellent fit to the central profile (NGC 4406, see Fig. 6
of Schweizer 1979).
Galaxies such as NGC 4406 and 4636 are good
candidates in which to pursue the search for nuclei.
*.
As Figure 20 shows, only a few of
King's galaxies have observed core radii which are much larger than
these false core radii. That is, M87, NGC 4649 and NGC 4472 are well
resolved, and NGC 4365 and 4636 are reasonably well resolved. Little
extra light can be hidden in the nuclei of these galaxies. And,
indeed, M87 did not successfully hide its core peculiarities
from
Young et al. (1978a),
nor does NGC 4636 appear isothermal in
Figure 19.
On the other hand, most galaxies in
Figure 20 fall close to the lines
describing the false cores. This means that their cores are not resolved
unambiguously. These galaxies could have isothermal cores, as illustrated
in Figure 19. However they could instead be
hiding nuclear brightness cusps as strong as those in
r1/4 laws. Furthermore, in at least one case where an
isothermal is a poor fit, a convolved r1/4
law gives an excellent fit to the central profile (NGC 4406, see Fig. 6
of Schweizer 1979).
Galaxies such as NGC 4406 and 4636 are good
candidates in which to pursue the search for nuclei.
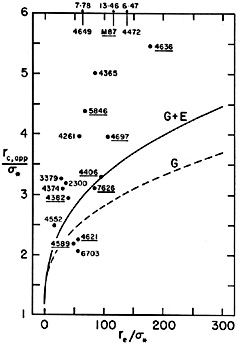 |
Figure 20. Resolution of E-galaxy cores,
here interpreted as the
degree to which we can distinguish isothermal cores from artificial
cores produced by seeing. The lines shown are for a convenient model
profile which has a significant nuclear light cusp, i.e., an
r1/4
law. Circularly symmetric r1/4 laws with effective radii
re have
been convolved with two point-spread functions, a pure Gaussian (G) and
a Gaussian core plus exponential wings which begin at 2.25
|
Given the fact that galaxies near the G + E line in
Figure 20
could be hiding nuclei, Schweizer assumes (by analogy with M31 and M32)
that they are generally hiding brightness cusps which are strong
enough to render the measured core parameters meaningless. I prefer the more
conservative assumption that most cores are nearly isothermal, by
analogy with the well-resolved cases NGC 4649, 4472 and 4365. Even M87
and NGC 4636 depart from isothermality by amounts which
are small enough that useful approximate values of rc
can still be derived.
If cores are isothermal then we can derive corrections for seeing as
given in Figure 21. These corrections are
manageably small if rc, app
 2.5
2.5 *.
I must emphasize that it is an assumption that
an isothermal and not an r1/4 law is generally valid
near the center.
Distinguishing conclusively between these alternatives will require
better resolution, perhaps even observations with Space Telescope.
*.
I must emphasize that it is an assumption that
an isothermal and not an r1/4 law is generally valid
near the center.
Distinguishing conclusively between these alternatives will require
better resolution, perhaps even observations with Space Telescope.
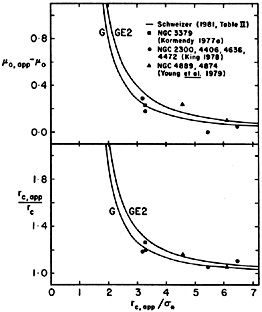 |
Figure 21. Seeing corrections to convert
apparent isothermal core radii rc, app and central
surface brightnesses µ0, app to true
values rc and µ0. The curves
labeled G and GE2 are calculated by
convolving isothermals with two point-spread functions, a Gaussian of
dispersion
|
Meanwhile, we can examine the internal physical consistency of the
assumption that cores are generally isothermal. For example,
Faber (1980)
has shown that more luminous galaxies have larger cores. In
fact, the well-resolved galaxies in Figure 20
are the most luminous
ones studied; this is one reason for suspecting that fainter ellipticals
just have smaller cores. However, consistency is not proof: the
false core radii given by seeing-convolved r1/4 laws
also correlate with luminosity
(Faber 1980).
The reason is that re determines
rc, app (Fig. 20), and
re depends on luminosity (equation 7). Another
interesting correlation is that between central velocity dispersion and
core radius (Fig. 22). This is a physically
reasonable result which, when combined with the
Faber-Jackson (1976)
relation and the virial
theorem, yields the plausible conclusion that the central mass-to-light
ratio M0/L0
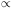 L0.26 (see
section 4.2.3). However, this
relation could also,
in principle, be spurious, through real relations between
L0.26 (see
section 4.2.3). However, this
relation could also,
in principle, be spurious, through real relations between
 , L
and re, and the seeing-induced dependence of
rc, app on re. Still, the
rc - L and rc -
, L
and re, and the seeing-induced dependence of
rc, app on re. Still, the
rc - L and rc -
 correlations are both
satisfied by galaxies which are well
enough resolved so that seeing effects are small. This fact, and the
physical consistency in the derived correlations provide some
additional support for the assumption that most ellipticals have nearly
isothermal cores. None of this changes the fact that many ellipticals
may harbor nuclei in addition to cores, and that some cores are
clearly not isothermal.
correlations are both
satisfied by galaxies which are well
enough resolved so that seeing effects are small. This fact, and the
physical consistency in the derived correlations provide some
additional support for the assumption that most ellipticals have nearly
isothermal cores. None of this changes the fact that many ellipticals
may harbor nuclei in addition to cores, and that some cores are
clearly not isothermal.
 |
Figure 22. Central velocity dispersion
versus core radius for
ellipticals and for the bulges of M31 and M81. The core radii have been
corrected for seeing effects as in
Figure 21. Seeing corrections
are large enough to be unreliable in galaxies with open symbols
(rc, app /
|
To conclude the discussion of isothermal cores, I list in Table 3 some benchmark core parameters for the densest nucleus studied to date and for a typical elliptical. The total light L and mass M in the core region are much larger in the elliptical. However, the central density is much larger in the nucleus of M31, because it is both small and bright. This high central density results in a short relaxation time; Tremaine and Ostriker (1982) derive a value of 3 × 109 yr, and discuss the possibility that a core collapse has occurred. In contrast, two-body relaxation is unlikely to be important in the cores of ellipticals. In particular, this does not seem to be a natural way to produce nuclear black holes.
| Parameter | M31 Nucleus | NGC 2300 |
| (densest observed) | (typical elliptical) | |
| rc | 1.4 pc | 370 pc |
| µ0 | 12.3 V mag arcsec-2 | 16.1 V mag arcsec-2 |
| L0 | 4 × 105
L pc-2
pc-2 |
1.4 × 104
L pc-2
pc-2 |
 |
181 ± 12 km s-1 | 235 ± 14 km s-1 |
 0 0 |
2.7 × 106
M pc-3
pc-3 |
66
M pc-3
pc-3 |
| M0 | 7.8 × 106
M pc-2
pc-2 |
4.9 × 104
M pc-2
pc-2 |
| M0 / L0 | 19 | 3.6 |
| Lproj(rc) | 1.7 × 106
L |
4.2 × 109
L |
| Mproj(rc) | 3.3 × 107
M |
1.5 × 1010
M |
NOTES. - The core radii
rc and the central surface brightnesses
µ0 and
L0 are derived by fitting the function
I(r) = I0(1 +
r2/rc2)-1 to
the photometry of
Light et al. (1974)
for M31 and of
King (1978)
for NGC 2300. These values are corrected for Galactic
absorption, and for
seeing (via Fig. 21). Both cores are only
moderately well resolved: rc, app /
| ||
Non-isothermal cores are of interest for several reasons. They may help us to refine our understanding of galaxy formation. For example, it would be useful to ask whether mergers leave any signature on core profiles, especially since they are so difficult to recognize using overall brightness profiles. However, the main interest in non-isothermal cores has centered on the possibility that they reveal the presence of nuclear black holes.
Significant dynamical evidence for a nuclear black hole was first
found in M87
(Young et al. 1978a,
Sargent et al. 1978,
hereafter
SYBSLH). This was an obvious galaxy for study because it is a strong
radio source with an optical jet, and because its core is so well
resolved that peculiarities should be hard to hide.
Young et al. (1978a)
have studied the core brightness profile; their excellent SIT
plus CCD data are shown in Figure 23. There is
a central point source,
which appears to be partly stellar and partly non-thermal
(Dressler 1980c).
In addition, there is a core between ~ 2" and
10" radius, but
one which maintains a significant brightness gradient even near the
center. It is this brightness gradient (and not the nucleus) which
suggests to Young and collaborators a model that contains a central
point mass, possibly a black hole, of mass ~ 3 × 109
M . A
similarly
non-isothermal core in the radio galaxy NGC 6251 can also be modeled
by assuming the existence of a nuclear black hole
(Young et al. 1979).
These observations fuel the widespread suspicion that massive black
holes might provide a natural engine to power nuclear activity.
. A
similarly
non-isothermal core in the radio galaxy NGC 6251 can also be modeled
by assuming the existence of a nuclear black hole
(Young et al. 1979).
These observations fuel the widespread suspicion that massive black
holes might provide a natural engine to power nuclear activity.
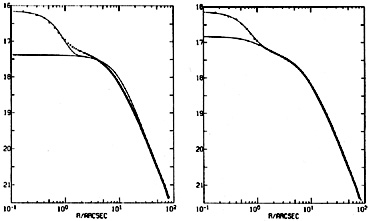 |
Figure 23. Fits of various model profiles
to the photometry (plus signs) of M87. These figures are taken from
Young et al. (1978a);
the photometry has been confirmed by
de Vaucouleurs and
Nieto (1979).
The left-hand panel shows that a King model plus a nuclear point source do
not fit the data. Some improvement would result from adopting a
smaller fitting range, but the observed profile between
10" and 2"
radius would still not turn down sharply enough into a core. The
right-hand panel shows that it is possible to fit the data with a
nuclear point source plus a King model modified to contain a central
black hole of mass ~ 3 × 109
M |
Further support for the black hole model was provided by the
observation of SYBSLH (see Figure 24) that
velocity dispersions
increase rapidly toward the center of M87. This increase was well
fitted by a King model with mass-to-light ratio 6.5 and a nuclear point
mass of ~ 5 × 109
M . It
was comforting to note that no such evidence
for a central point mass was seen in the comparison galaxy NGC 3379,
which has an isothermal core. However, more recent work has weakened
the force of these conclusions. First,
Illingworth (1981)
has shown that the velocity dispersion gradient in M87 is in fact similar to that
in the isothermal cores of NGC 3379 and NGC 4472
(Fig. 35). Also,
Dressler (1980c)
has remeasured the nuclear dispersion in M87 in
well-defined and excellent seeing (0.75" diameter images
in a 1" × 1"
aperture, compared with 5.4" resolution in SYBSLH). He obtains a
dispersion which is much smaller than the inward extrapolation of the
SYBSLH model (see Fig. 24). A massive central
black hole is still
possible if the nuclear star cluster is large enough (i.e., barely
unresolved). However, the model is no longer compelling. Finally,
Duncan and Wheeler
(1980)
and Binney and Mamon
(1982)
note that the
interpretation of the data is very model-dependent. If the assumption
of an isotropic velocity distribution is relaxed, then it is possible
to model the observations without using a black hole (see
Binney 1982a
for a review). Therefore, it is not yet observationally clear whether
nuclear black holes exist.
. It
was comforting to note that no such evidence
for a central point mass was seen in the comparison galaxy NGC 3379,
which has an isothermal core. However, more recent work has weakened
the force of these conclusions. First,
Illingworth (1981)
has shown that the velocity dispersion gradient in M87 is in fact similar to that
in the isothermal cores of NGC 3379 and NGC 4472
(Fig. 35). Also,
Dressler (1980c)
has remeasured the nuclear dispersion in M87 in
well-defined and excellent seeing (0.75" diameter images
in a 1" × 1"
aperture, compared with 5.4" resolution in SYBSLH). He obtains a
dispersion which is much smaller than the inward extrapolation of the
SYBSLH model (see Fig. 24). A massive central
black hole is still
possible if the nuclear star cluster is large enough (i.e., barely
unresolved). However, the model is no longer compelling. Finally,
Duncan and Wheeler
(1980)
and Binney and Mamon
(1982)
note that the
interpretation of the data is very model-dependent. If the assumption
of an isotropic velocity distribution is relaxed, then it is possible
to model the observations without using a black hole (see
Binney 1982a
for a review). Therefore, it is not yet observationally clear whether
nuclear black holes exist.
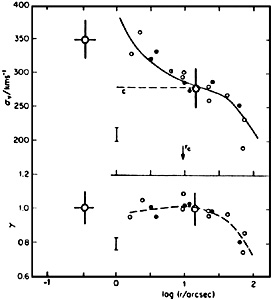 |
Figure 24. Velocity dispersions
|
Another galaxy whose central profile departs from an isothermal is
NGC 1316 = Fornax A. In
section 3.3.7 I discussed
Schweizer's (1981b)
conclusion that this galaxy is a merger remnant. Schweizer shows further
that the brightness profile at r < 5" deviates above the
inward extrapolation of an r1/4 law fitted at larger
radii. This extra light is well described by a
King (1966)
model with log (rt / rc)
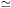 2.65. Such a
model has a very pronounced core-halo structure. Normal ellipticals
have log (rt / rc)
2.65. Such a
model has a very pronounced core-halo structure. Normal ellipticals
have log (rt / rc)
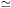 2.25, a value which
gives a profile like an r1/4
law (Kormendy 1977c;
King 1978).
Corrected for seeing, the core radius
in NGC 1316 is rc
2.25, a value which
gives a profile like an r1/4
law (Kormendy 1977c;
King 1978).
Corrected for seeing, the core radius
in NGC 1316 is rc
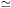 0.6" ± 0.2" or
0.10 ± 0.03 kpc (H0 = 50 km
s-1 Mpc-1). This is a surprisingly small value for
a galaxy with
MV
0.6" ± 0.2" or
0.10 ± 0.03 kpc (H0 = 50 km
s-1 Mpc-1). This is a surprisingly small value for
a galaxy with
MV 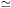 -23.8. For comparison, rc
-23.8. For comparison, rc
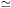 0.06 kpc in
the bulge of M31
(Mv, bulge = -19.6). Typical ellipticals in
King (1978)
have 0.1
0.06 kpc in
the bulge of M31
(Mv, bulge = -19.6). Typical ellipticals in
King (1978)
have 0.1 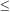 rc
rc
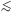 1.0 kpc (see
Fig. 22) and
-21.5
1.0 kpc (see
Fig. 22) and
-21.5  MV
MV
 - 23.5.
Young et al. (1979)
find still larger cores in ellipticals comparable in luminosity
to NGC 1316: rc ~ 2.1 kpc in NGC 4874
(MV ~ -23.9);rc ~ 1.7 kpc in
NGC 4889 (MV ~ -24.4), and
rc ~ 1.0 kpc in NGC 6251. Schweizer points
out that a core as small as that in NGC 1316 would be unresolved in
these distant ellipticals. However, as discussed above, many of the
observed large cores appear to be real. Then NGC 1316 has an
anomalously small core for its luminosity.
- 23.5.
Young et al. (1979)
find still larger cores in ellipticals comparable in luminosity
to NGC 1316: rc ~ 2.1 kpc in NGC 4874
(MV ~ -23.9);rc ~ 1.7 kpc in
NGC 4889 (MV ~ -24.4), and
rc ~ 1.0 kpc in NGC 6251. Schweizer points
out that a core as small as that in NGC 1316 would be unresolved in
these distant ellipticals. However, as discussed above, many of the
observed large cores appear to be real. Then NGC 1316 has an
anomalously small core for its luminosity.
The properties of non-isothermal cores, and particularly the above observations, motivate the following question (see also section 4.2.5, and Hausman and Ostriker 1978; cf. Schweizer 1981b). Could a non-isothermal core be the signature of a merger of two galaxies which had very different core radii? That is, did part of the small core survive the merger to produce a "core within a core"? This process would be similar in principle to the possible building of galactic nuclei out of globular clusters through dynamical friction (Tremaine, Ostriker and Spitzer 1975; Tremaine and Ostriker 1982). It is particularly attractive for NGC 1316, which is suggested to be a merger remnant. The survival of small cores which are being eaten is not implausible in view of the high central surface brightnesses µ0 of small ellipticals. For example, M32 has µ0 ~ 14.7 B mag arcsec-2 (Bendinelli et al. 1977), compared with an average <µ0> = 16.9 B mag arcsec-2 (dispersion = 0.7 mag arcsec-2) for King's (1978) ellipticals. The core of M32 is also tightly bound; rc ~ 8 pc (Walker 1962) compared with core radii of 0.1 - 1.0 kpc for large ellipticals. Finally, the parameters given in Table 3, and especially the high central density of the M31 nucleus, suggest that this nucleus, for example, might be robust enough to survive ingestion by NGC 2300. It would be worth looking further into the possibility that some cores might be non-isothermal because of mergers, especially in view of the insensitivity of overall profiles to merger processes.