4.2.3. Central Velocity Dispersions. II. Mass-to-Light Ratios

Since elliptical galaxies contain little material in nearly circular orbits, their masses are usually calculated using central velocity dispersions and the virial theorem. A review of such mass determinations is given in Faber and Gallagher (1979). However, total masses can be calculated only by assuming that the mass-to-light ratio M/L is the same everywhere in the galaxy, and that the velocity distribution is everywhere isotropic with constant . These assumptions are probably not correct. Therefore, only core mass-to-light ratios will be discussed in this section. Their determination requires fewer and better-justified assumptions (King and Minkowski 1972; Faber and Gallagher 1979), although not ones which are observationally verified. If the velocity distribution is strongly anisotropic near the center, then even these masses will be greatly in error (Binney and Mamon 1982; Tremaine and Ostriker 1982; see since 3.3.8).

If we assume that cores are isothermal, then the virial theorem gives central mass-to-light ratios

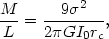(21)

where I₀ is the central surface brightness (King 1966; Schechter 1980). Conveniently, the combination I₀r_c is relatively insensitive to seeing. At present M/L values can be calculated for only a few galaxies because there is not enough published photometry. For 17 giant ellipticals, Schechter (1980) finds an average value of <M/L_B> = 7.8 (dispersion = 3.2) in solar units. (Here I have corrected the values for NGC 4552 and 4636 for photometric zero-point errors in King 1978; see Boroson and Kormendy 1982). The only disk-galaxy bulge for which there exists sufficient photometry is M31; Faber and Gallagher (1979) obtain M/L_B = 8.5. If we briefly relax our adopted restriction and consider global M/L determinations, then there exist slightly more data. Faber and Gallagher (1979) obtain <M/L_B> = 7.8 ± 1.3 for five additional (S0) bulges. The data are very sparse but there seems to be considerable homogeneity in these stellar populations.

One question of considerable interest is the possible dependence of M/L on L. With data on only a score of galaxies, a plot of M/L versus L (Schechter 1980, Fig.2) has so much scatter that any weak luminosity dependence is masked. However, we can look for a luminosity dependence using mean relations between core parameters. Faber and Jackson (1976) combined the L 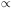⁴ relation with other power-law relations (not explicitly stated) between I₀, r_c and L to derive M/L 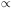L^0.5. On the other hand, S²BS assumed that all galaxies have the same surface brightness, in which case the relation L 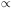⁴ and the virial theorem M 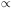² r_c imply that M/L 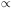L⁰. Other determinations include M/L 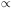L^1/8 (Schechter and Gunn 1978) and M/L 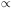L^0.34 (Michard 1980, for global mass-to-light ratios).

The mean parameter correlations derived in this paper allow a new determination of the luminosity dependence of M/L. The required relations are (1) L 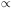^5.4 from section 4.2.2, (2) 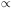r_c^0.25 from Figure 22, (3) a similar relation I₀ 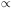r_c^-0.87, not illustrated but derived in the same way as (2), and (4) the virial theorem, M/L 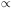² / I₀r_c. Combining these gives

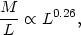(22)

intermediate between the results of Faber and Jackson (1976) and of S²BS and Schechter (1980). Note that if we assume that L 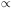⁴, then the above relation becomes M/L 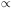L^0.49, in agreement with Faber and Jackson.

The above weak dependence of M/L on L is consistent with Tinsley's (1978) population models of elliptical galaxies. These model the observed color-magnitude relations by varying the metallicity (cf. Michard 1980). Tinsley predicts that M/L 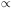L^0.13, which is certainly consistent with equation (22) in view of the small sample of data. This is a reassuring indication. However, there is a clear need for data on more than ~ 20 galaxies, with a greater range of luminosity than is represented in current measurements.