


4.2.4. Central Velocity Dispersions.
III. Correlation With Line Strength
The parameter correlations discussed so far suggest that the
properties of elliptical galaxies are largely controlled by one parameter,
the total luminosity L (e.g.,
Faber 1973b).
Core parameters correlate
closely with L; these include central velocity dispersion, core radius,
central surface brightness and metallicity
(6)
Also correlating with L,
although with larger scatter, are global parameters such as the effective
radius and surface brightness
(section 3.3.3) and a measure
(V/ )*
of the dynamical importance of rotation versus random motions
(section 4.2.6).
However, a closer examination of the
log
)*
of the dynamical importance of rotation versus random motions
(section 4.2.6).
However, a closer examination of the
log -
MB and Mg2 - MB
correlations suggests that a second parameter is at work. This result
(Terlevich et al. 1981)
is summarized in Figure 34.
-
MB and Mg2 - MB
correlations suggests that a second parameter is at work. This result
(Terlevich et al. 1981)
is summarized in Figure 34.
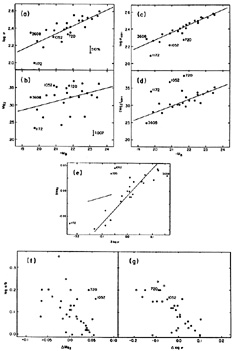 |
Figure 34. Parameter plots from
Terlevich et
al. (1981)
illustrating the probable two-parameter nature of elliptical
galaxies. Panels (a) - (d) show correlations with absolute magnitude
MB of the logarithm of the velocity dispersion,
log |
The correlation of
 Mg2
and
Mg2
and  log
log implies
that the galaxies occupy a canted surface in
log
implies
that the galaxies occupy a canted surface in
log -
Mg2 - MB
space. A combined least-squares fit yields
-
Mg2 - MB
space. A combined least-squares fit yields
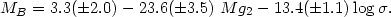 |
(23) |
The individual relations corrected for the second parameter (Fig. 34c,d) are:
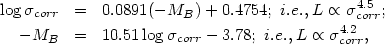 |
(24) |
using MB and
log corr as
independent variables, respectively;
corr as
independent variables, respectively;
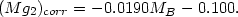 |
(25) |
Figure 34 suggests that the second parameter
may be related to the
intrinsic axial ratio. On average, apparently rounder galaxies have
higher  and stronger
metal lines than flatter galaxies (cf.
van den Bergh's 1979
result that rounder galaxies are redder). Note that
projection effects should fill in the region below the correlations in
Figure 34 (f) and
(g) with intrinsically flattened galaxies that are
seen nearly face-on.
and stronger
metal lines than flatter galaxies (cf.
van den Bergh's 1979
result that rounder galaxies are redder). Note that
projection effects should fill in the region below the correlations in
Figure 34 (f) and
(g) with intrinsically flattened galaxies that are
seen nearly face-on.
The above results have been criticized by
Tonry and Davis
(1981b),
who do not confirm the correlations with axial ratio. They suggest
that log and Mg2
do not separately correlate with MB. Instead,
they believe that the
and Mg2
do not separately correlate with MB. Instead,
they believe that the
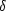 log
log -
-
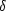 Mg2
relation is driven by a correlation between
log
Mg2
relation is driven by a correlation between
log and
Mg2. Such a correlation does exist. When plotted
using parameters from
Terlevich et al. (1981)
the scatter is even
consistent with the measuring errors, a result which supports Tonry and
Davis' suggestion. In fact, the scatter is produced in part by the
dispersion in MB (the "second parameter" in this
plot). Thus it may be that the true second parameter in ellipticals is
related to Mg2 or
log
and
Mg2. Such a correlation does exist. When plotted
using parameters from
Terlevich et al. (1981)
the scatter is even
consistent with the measuring errors, a result which supports Tonry and
Davis' suggestion. In fact, the scatter is produced in part by the
dispersion in MB (the "second parameter" in this
plot). Thus it may be that the true second parameter in ellipticals is
related to Mg2 or
log as well as being
related to flattening. However, flattening does
seem to be involved in the second parameter (Tonry and Davis apparently
did not find any correlations with flattening because their measuring
errors were too large,
Davies 1982).
The above discussion is consistent with
Terlevich et
al. (1981),
who state their conclusions cautiously.
as well as being
related to flattening. However, flattening does
seem to be involved in the second parameter (Tonry and Davis apparently
did not find any correlations with flattening because their measuring
errors were too large,
Davies 1982).
The above discussion is consistent with
Terlevich et
al. (1981),
who state their conclusions cautiously.
The correlations of Figure 34 contain information about the true shapes of ellipticals, although they are difficult to interpret because intrinsic correlations with flattening as well as the viewing geometry may be involved. The parameter relations also have implications for theories of galaxy formation, being generally easier to reconcile with dissipational-collapse theories than with dissipationless formation. Our understanding of these implications is very rudimentary. Besides enlarging the galaxy sample, we need to explore correlations with parameters which measure more global dynamical quantities.
Panels (f) and (g) suggest that the second parameter may be
related to intrinsic axial ratio. They show correlations between the
logarithm of the observed axial ratio a/b and deviations
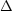 Mg2 and
Mg2 and
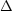 log
log from the corrected relations (c), (d). Only galaxies brighter than
MB
from the corrected relations (c), (d). Only galaxies brighter than
MB 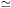 -
20 are illustrated; fainter galaxies tend to be more
heterogeneous in their stellar populations
(Faber 1977)
and show weaker correlations with log(a/b).
-
20 are illustrated; fainter galaxies tend to be more
heterogeneous in their stellar populations
(Faber 1977)
and show weaker correlations with log(a/b).
6 The metallicity is measured using an index Mg2 of the strength of Mg I "b" plus MgH at ~ 5178Å, see Faber, Burstein and Dressler (1977). The calibration of Mg2 (in mag) is [Fe/H] = 3.9 Mg2 - 0.9, where [Fe/H] is the logarithmic metal, abundance relative to the sun (Burstein 1979a; Terlevich et al. 1981). Further discussion of Mg2 is found in references given in Terlevich et al. (1981). The Mg2 - MB correlation is illustrated in Fig. 1 of Faber (1977). Back.