3. STELLAR POPULATION MODELLING: THE PARAMETRIC APPROACH AND ITS LIMITATIONS

The parametric description of the stellar luminosity PDF is the one used by far the most often, although usually only the mean value of the distribution is computed. In fact, when we weight the stellar luminosity along an isochrone with an IMF in an SSP, it is such a mean value, µ₁'(ℓ_i), that is obtained (see Cerviño and Luridiana 2006 for more details).

We can also evaluate by how much the possible ℓ_i values differ from the mean value. For example, the variance µ₂(ℓ_i), which is the average of the square of the distance to the mean (i.e. e integral of (ℓ_i - µ₁'(ℓ_i))² (ℓ_i) over the possible ℓ_i values). In general, we can compute the difference between the mean and the possible ℓ_i elements of the distribution using any power, (ℓ_i - µ₁'(ℓ_i))ⁿ, and the resulting parameter is called the central n-moment, µ_n(ℓ_i). We can also obtain the covariance for two different luminosities ℓ_i and ℓ_j by computing (ℓ_i - µ₁'(ℓ_i))ⁿ(ℓ_j - µ₁'(ℓ_j))^m integrated over (ℓ_i, ℓ_j), where linear covariance coefficients are obtained for the case n = m = 1.

Parametric descriptions of PDFs usually use few parameters: the mean, variance, skewness, ₁(ℓ_i) = µ₃ / µ₂^3/2, and kurtosis ₂(ℓ_i) = µ₄ / µ₂² -3. Skewness is a measure of the asymmetry of the PDF. Kurtosis can be interpreted as a measure of how flat or peaked a distribution is (if we focus the comparison on the central part of the distribution) or how fat the tails of the distribution are (if we focus on the extremes) when compared to a Gaussian distribution. For reference, a Gaussian distribution has ₁ = ₂ = 0. Typical values of the four parameters and their evolution with time for an SSP case are shown in Fig. 3 taken from Cerviño and Luridiana (2006).

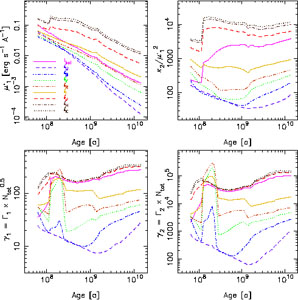Figure 3. Main parameters of the luminosity function in several photometric bands. Figure from Cerviño and Luridiana (2006). In the notation used in this paper, 2 refers to µ2, 1 refers to 1;(Li), and 2 refers to 2;(Li).

The parameters that describe the distribution of integrated luminosities, (L₁, ...,L_n; t_mod), are related to those of the stellar luminosity function by simple scale relations (Cerviño and Luridiana 2006):

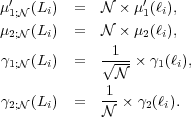(1) (2) (3) (4)

We can then obtain additional scale relations for the effective number of stars at a given luminosity, N_eff; (L_i) (Buzzoni 1989), the SBF, 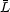(Tonry and Schneider 1988, Buzzoni 1993), and the correlation coefficients between two different luminosities, 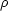(L_i, L_j):

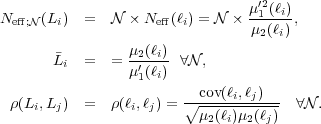(5) (6) (7)

Direct (and simple) computation of the parameters of the distribution provides several interesting results. First, SBFs are a measure of the scatter that is independent of and can be applied to any situation (from stellar clusters to galaxies) in fitting techniques. Second, correlation coefficients are also invariant about and can be included in any fitting technique. Third, since the inverse of N_eff; (L_i) is the relative dispersion, when → ∞ the relative dispersion goes to zero, although the absolute dispersion (square root of the variance, ) goes to infinity. Fourth, when → ∞, _1;(L_i) and _2;(L_i) goes to zero, and hence the shape of the distribution of integrated luminosities becomes a Gaussian-like distribution (actually an n-dimensional Gaussian distribution including the corresponding (L_i, L_j) coefficients). We can also obtain the range of _1;(L_i) and _2;(L_i) values for which the distribution can be approximated by a Gaussian or an expansion of Gaussian distributions (such an Edgeworth distribution) for a certain luminosity interval. As reference values, the shape of PDFs where _1; < 0.3 or _2; < 0.1 are well described with these four parameters by an Edgeworth distribution; when _1; < 0.03 and _2; < 0.1, the PDFs are well described by a Gaussian distribution with the corresponding mean and variance. A Monte Carlo simulation or a convolution process is needed in other situations. The possible situations are shown in Fig. 4, taken from Cerviño and Luridiana (2006).

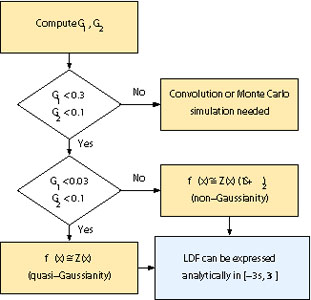Figure 4. Characterization of a PDF based on Edgeworth's approximation to the second order and a Gaussianity tolerance interval of ± 10%. Figure taken from Cerviño and Luridiana (2006), where 1 refers to 1;(Li) and 2 refers to 2;(Li).

Another possibility that covers situations for higher _1; and _2; values quoted here (i.e. asymmetric PDFs) is to approximate (ℓ_i) by gamma distributions, as done by Maíz Apellániz (2009). This approach can be used in a wide variety of situations as long as the PDF has no bumps or the bumps are smooth enough and an accurate description of the tails of the distribution is not required.

3.1. The mean and variance obtained using standard models

We have seen that using Eq. (1), the mean value can be expressed for any possible value or for any quantity related to . Most population synthesis codes use the mass of gas transformed into stars or the star formation rate (also expressed as the amount of mass transformed into stars over a time interval) instead of referring to the number of stars. Hence, the typical unit of luminosity is [erg s^-1 M^-1] or something similar. However, here I argue that the computed value actually refers to the mean value of _ℓ(ℓ), so the units of the luminosity obtained by the codes should be [erg s^-1] and refer to individual stars.

In fact, the difference is in the interpretation and algebraic manipulation of 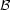(m₀, t, Z) and the IMF. The usual argument has two distinct steps. (1) The integrated luminosity and total stellar mass in a system are the sum of the luminosities and masses of all the individual stars in the system. Thus, the ratio of luminosity to mass produces the mass-luminosity relation for the system. (2) 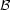(m₀, t, Z) (or the IMF) provides the actual mass of the individual stars in the system, and since the shape of such functions is independent of the number of stars in the system, the previous mass-luminosity relations are valid for any ensemble of stars with similar 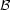(m₀, t, Z) functional form. The first step is always true as long as we know the masses and evolutionary status of all the stars in the system (actually it is the way that each individual Monte Carlo simulation obtains observables). The second step is false: we do not know the individual stars in the system. We can describe the set using a probability distribution, and hence we can describe the integrated luminosity of all possible combinations of a sample of individual stars.

It is trivial to see that the mass normalisation constant used in most synthesis codes is actually the mean stellar mass µ'₁(m₀) obtained using the IMF as a PDF. ² Equivalently, total masses or star formation rates obtained using inferences from synthesis models are actually × µ'₁(m₀) and × µ'₁(m₀) × t^-1. Usually, this difference has no implication; however, it is different to say that a galaxy has a formation rate of, say, 0.1 stars per year (it forms, on average, a star every 10 years whatever its mass) than 0.1 M per year (does this mean that, on average, 10³ years are needed to form a 100-M star without forming any other star?).

Different renormalisations are performed on a physical basis, depending on the system we are interested in. Low-mass stars in young starbursts make almost no contribution to the UV integrated luminosity, so we can exclude low-mass stars from the modelling. Massive stars are not present in old systems; hence, we do not need to include massive stars in these SSP models. The use of different normalisations can be solved easily using a renormalisation process. Hence, we can compare the mean values obtained from two synthesis codes that use different constraints. However, we must be aware that underlying any such renormalisation there are different constraints on 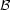(m₀, t, Z), and hence there are changes in the shape of the possible 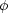(ℓ₁, ..., ℓ_n; t_mod), such as the absence or presence of a Dirac delta function at ℓ_i = 0. 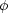This affects the possible values of the mean, variance (SBF or N_eft), skewness, and kurtosis used to describe (L₁, ...,L_n; t_mod).

² For reference, a Salpeter IMF in the mass range 0.08-120 M has µ'₁(m₀) = 0.28 M, µ₂(m₀) = 1.44, ₁(m₀) = 1691.47, and ₂(m₀) = 2556.66. This implies that the distribution of the total mass becomes Gaussian-like for ~ 3 × 10⁷ stars when the average total mass is approximately 9 × 10⁶ M. Back.